
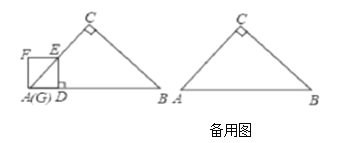
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,线段
,线段![]() 上一动点
上一动点![]() ,以
,以![]() 的速度从点
的速度从点![]() 出发向终点
出发向终点![]() 运动.过点
运动.过点![]() 作
作![]() ,交折线
,交折线![]() 于点
于点![]() ,以
,以![]() 为一边,在
为一边,在![]() 左侧作正方形
左侧作正方形![]() .设运动时间为
.设运动时间为![]()
![]() ,正方形
,正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() .
.
(1)![]() ________
________![]() ;
;
(2)当![]() 为何值时,点
为何值时,点![]() 在
在![]() 上;
上;
(3)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)直线![]() 将
将![]() 面积分成
面积分成![]() 两部分时,直接写出
两部分时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)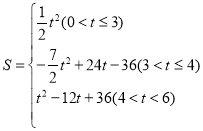 ;(4)当点E在AC上时,
;(4)当点E在AC上时,![]() ;当点E在BC上时,
;当点E在BC上时,![]()
【解析】
(1)根据题意,设AC长为![]() ,然后利用勾股定理进一步列出方程求解即可;
,然后利用勾股定理进一步列出方程求解即可;
(2)根据题意,画出当点F在AC上时的图形,然后证明出AG=DG=BD=![]() AB=2,最后进一步计算即可;
AB=2,最后进一步计算即可;
(3)根据题意,分当![]() 时、
时、![]() 时、当
时、当![]() 时三种情况,分别得出相应的图形,然后根据图形进一步计算求解即可;
时三种情况,分别得出相应的图形,然后根据图形进一步计算求解即可;
(4)如图所示,①当点E在AC上时,画出此时的正方形DEFG,连接BF交AC于点M,
根据题意首先求出![]() ,然后进一步证明△FEM~△BAM,接着利用相似三角形性质进一步求解即可;②当点E在BC上时,
,然后进一步证明△FEM~△BAM,接着利用相似三角形性质进一步求解即可;②当点E在BC上时,![]() ,画出此时的正方形DEFG,延长BF交AC于点M,过点F作FN⊥BC交BC于N,首先根据等腰直角三角形性质得出BD=DE=EF=
,画出此时的正方形DEFG,延长BF交AC于点M,过点F作FN⊥BC交BC于N,首先根据等腰直角三角形性质得出BD=DE=EF=![]() ,NE=FN=
,NE=FN=![]() ,然后进一步证明△BFN~△BMC,从而得出
,然后进一步证明△BFN~△BMC,从而得出![]() ,由此进一步分析即可得知当直线
,由此进一步分析即可得知当直线![]() 将
将![]() 面积分成
面积分成![]() 两部分时的
两部分时的![]() 的取值范围.
的取值范围.
(1)设AC长为![]() ,则BC=
,则BC=![]() ,
,
则在Rt△ABC中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
∵![]() 是正数,
是正数,
∴![]() ,
,
∴AC=![]() ,
,
故答案为:![]() ;
;
(2)当点F在AB上时,可得下图:
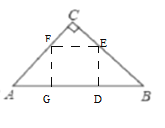
∵四边形DEFG是正方形,
∴EF∥AB,EF=FG=GD=ED,∠FGA=∠EDB=90°,
∵在Rt△ABC中,AC=BC,∠C=90°,
∴∠B=∠A=45°,
∴△AGF与△BDE是等腰直角三角形,
∴AG=GF,DE=BD,
∴AG=DG=BD=![]() AB=2,
AB=2,
∴AD=4,
∴此时![]() ;
;
(3)如图,当![]() 时,重叠部分为△ADE,
时,重叠部分为△ADE,
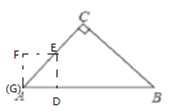
∵∠C=90°,AC=BC,
∴∠CAB=∠B=45°,
∵DE⊥AB,
∴∠AED=45°,
∴AD=DE=![]() ,
,
∴![]() ;
;
如图,当![]() 时,重叠部分是五边形MNEDG,
时,重叠部分是五边形MNEDG,
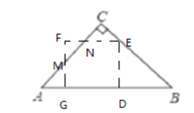
∵四边形DEFG是正方形,
∴FG=GD=DE,∠AGM=∠EDB=∠F=90°,
∵∠B=∠A=45°,
∴∠AMG=∠DEB=45°,
∴AG=GM,BD=DE,
∴FG=DG=DE=DB=![]() ,
,
∴MG=AG=ADDG=![]() ,
,
∴FM=FGMG=![]() ,
,
∵∠AMG=45°,∠F=90°,
∴∠FNM=45°,
∴FN=FM=![]() ,
,
∴
如图,当![]() 时,重叠部分为正方形DEFG,
时,重叠部分为正方形DEFG,
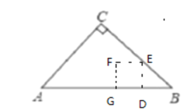
∵四边形DEFG是正方形,
∴GD=DE,∠EDB=90°,
∵∠B=45°,
∴∠DEB=45°,
∴DE=DB=![]() ,
,
∴![]() ,
,
综上所述,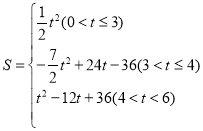 ;
;
(4)

①如上图所示,当点E在AC上时,画出此时的正方形DEFG,连接BF交AC于点M,
∵要使直线![]() 将
将![]() 面积分成
面积分成![]() 两部分,
两部分,
∴此时![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵EF∥AB,
∴∠FEM=∠BAM,
∴△FEM~△BAM,
∴![]() ,
,
又∵在等腰Rt△ADE中,AE=![]() ,
,
∴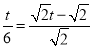 ,
,
∴![]() ;
;
②如上图所示,当点E在BC上时,![]() ,画出此时的正方形DEFG,延长BF交AC于点M,过点F作FN⊥BC交BC于N,
,画出此时的正方形DEFG,延长BF交AC于点M,过点F作FN⊥BC交BC于N,
则BD=DE=EF=![]() ,
,
在Rt△BDE中,∠ABC=45°,
∴BE=![]() BD=
BD=![]() ,
,
∵EF∥AB,
∴∠NEF=∠CBA=45°,
∵FN⊥BC,
∴△FNE为等腰直角三角形,
∴NE=FN=![]() ,
,
∵∠C=∠FNB,∠CBM=∠NBF,
∴△BFN~△BMC,
∴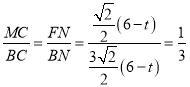 ,
,
∵AC=BC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当直线![]() 将
将![]() 面积分成
面积分成![]() 两部分时,
两部分时,![]() ,
,
综上所述,当点E在AC上时,![]() ;当点E在BC上时,
;当点E在BC上时,![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
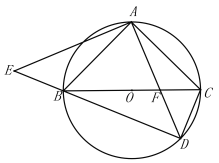
【题目】如图,在△ABC中,![]() ,BC为
,BC为![]() 的直径,D为
的直径,D为![]() 任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
(1)求证:△ABE≌△ACD;
(2)填空:①当∠CAD的度数为 时,四边形ABDC是正方形;
②若四边形ABDC的面积为4,则AD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
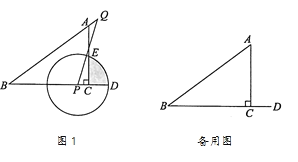
【题目】如图1,△ABC中,∠ACB=90°,AC=3,BC=4,延长BC到点D,使BD=BA,P是BC边上一点.点Q在射线BA上,PQ=BP,以点P为圆心,PD长为半径作⊙P,交AC于点E,连接PQ,设PC=x.
(1)AB= ,CD= ,当点Q在⊙P上时,求x的值;
(2)x为何值时,⊙P与AB相切?
(3)当PC=CD时,求阴影部分的面积;
(4)若⊙P与△ABC的三边有两个公共点,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
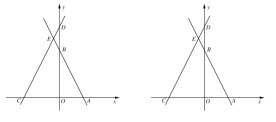
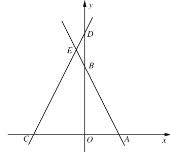
【题目】在平面直角坐标系中,点O为坐标原点,直线![]() 与x,y轴分别交于点A,B两点,直线y=2x+3m与
与x,y轴分别交于点A,B两点,直线y=2x+3m与![]() 轴分别交于
轴分别交于![]() 两点,两直线交于点E,点P在射线CA上,点Q在射线AE上,分别连接
两点,两直线交于点E,点P在射线CA上,点Q在射线AE上,分别连接![]() 交于点F,且
交于点F,且![]() .
.
(1)若点E的横坐标为![]() ,求
,求![]() 的值
的值
(2)当![]() 时,过点P作
时,过点P作![]() 于点M,过点E作
于点M,过点E作![]() 于点N,求证:
于点N,求证:![]()
(3)在(1)的条件下,当![]() 时,过点P作
时,过点P作![]() 交AB于点G,点K在射线CQ上,射线EK交直线
交AB于点G,点K在射线CQ上,射线EK交直线![]() 于点L,射线
于点L,射线![]() 交直线
交直线![]() 于点R,连接
于点R,连接![]() ,当
,当![]() 时,求K点LR到的距离.
时,求K点LR到的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
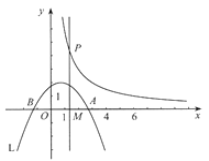
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
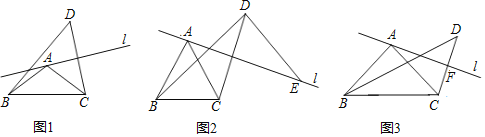
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为______.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD.
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士在谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:80 85 90 95 90 95 90 65 75 100 90 70 95 90 80 80 90 95 60 100
乙小区:60 80 95 80 90 65 80 85 85 100 80 95 90 80 90 70 80 90 75 100
整理数据
成绩 小区 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
数据名称 计量小区 | 平均数 | 中位数 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() =______,
=______,![]() =______;
=______;
(2)若乙小区共有1200人参与答卷,请估计乙小区成绩大于90分的人数;
(3)社区管理人员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理人员的理由;为了更好地宣传新型冠状病毒肺炎防护知识,社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训,请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宝网店销售甲、乙两种电器,已知甲种电器每个的售价比乙种电器多60元,马老师从该网店购买了3个甲种电器和2个乙种电器,共花费780元.
(1)该店甲、乙两种电器每个的售价各是多少元?
(2)根据销售情况,店主决定用不少于10800元的资金购进甲、乙两种电器,这两种电器共100个,已知甲种电器每个的进价为150元,乙种电器每个的进价为80元.若所购进电器均可全部售出,请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com