
【题目】马山被誉为“中国民间文化艺术之乡”,马山的民族文化丰富多彩,形式多样.为了了解某学学生对马山民族文化的喜爱情况,某校开展了“我最喜爱的民俗活动”调查问卷,其中包括:![]() 壮族三声部民歌,
壮族三声部民歌,![]() 壮族扁担舞,
壮族扁担舞,![]() 会鼓,
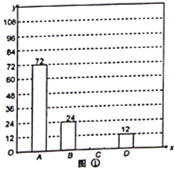
会鼓,![]() 采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
(1)这次抽样调查中,一共抽查了名学生,![]() 项所对应圆心角的度数为;
项所对应圆心角的度数为;
(2)请补全条形统计图;
(3)若九(1)班要从甲、乙、丙和丁这四人中选两个人参与调查,请用列表法或画树状图法求出恰好选中甲乙的概率.

【答案】(1)120,![]() ;(2)见解析;(3)见解析,
;(2)见解析;(3)见解析,![]()
【解析】
(1)根据![]() 壮族三声部民歌的人数及所占的百分比计算总人数,进而计算
壮族三声部民歌的人数及所占的百分比计算总人数,进而计算![]() 项所对应圆心角的度数;
项所对应圆心角的度数;
(2)根据120×10%=12人,补全条形统计图即可;
(3)利用列表法或画树状图法列出所有的可能,再根据概率公式计算即可.
解:(1)72÷60%=120(人),
![]() 项所对应圆心角的度数为:
项所对应圆心角的度数为:![]() =36°
=36°
故答案为:120,![]() .
.
(2)补全条形统计图如图:
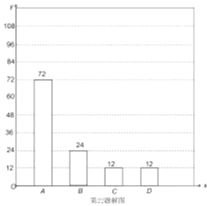
(3)列表如下:
甲 | 乙 | 丙 | 丁 | |
甲 | (乙,甲) | (丙,甲) | (丁,甲) | |
乙 | (甲,乙) | (丙,乙) | (丁,乙) | |
丙 | (甲,丙) | (乙,丙) | (丁,丙) | |
丁 | (甲,丁) | (乙,丁) | (丙,丁) |
或画树状图如下:
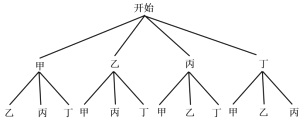
由列表(树状图)可知,共有12种等可能的结果,其中恰好选中甲乙的结果有2种.
∴![]() (恰好选中甲乙)
(恰好选中甲乙)![]()


科目:初中数学 来源: 题型:
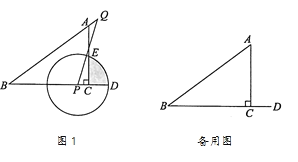
【题目】如图1,△ABC中,∠ACB=90°,AC=3,BC=4,延长BC到点D,使BD=BA,P是BC边上一点.点Q在射线BA上,PQ=BP,以点P为圆心,PD长为半径作⊙P,交AC于点E,连接PQ,设PC=x.
(1)AB= ,CD= ,当点Q在⊙P上时,求x的值;
(2)x为何值时,⊙P与AB相切?
(3)当PC=CD时,求阴影部分的面积;
(4)若⊙P与△ABC的三边有两个公共点,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为______.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD.
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值.
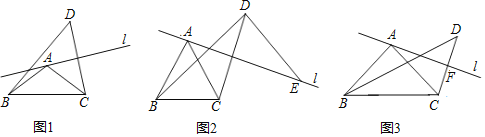
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士在谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:80 85 90 95 90 95 90 65 75 100 90 70 95 90 80 80 90 95 60 100
乙小区:60 80 95 80 90 65 80 85 85 100 80 95 90 80 90 70 80 90 75 100
整理数据
成绩 小区 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
数据名称 计量小区 | 平均数 | 中位数 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() =______,
=______,![]() =______;
=______;
(2)若乙小区共有1200人参与答卷,请估计乙小区成绩大于90分的人数;
(3)社区管理人员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理人员的理由;为了更好地宣传新型冠状病毒肺炎防护知识,社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训,请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
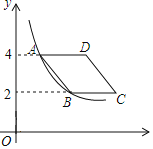
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
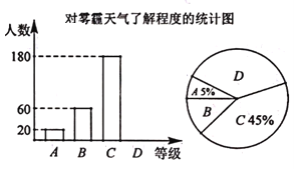
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宝网店销售甲、乙两种电器,已知甲种电器每个的售价比乙种电器多60元,马老师从该网店购买了3个甲种电器和2个乙种电器,共花费780元.
(1)该店甲、乙两种电器每个的售价各是多少元?
(2)根据销售情况,店主决定用不少于10800元的资金购进甲、乙两种电器,这两种电器共100个,已知甲种电器每个的进价为150元,乙种电器每个的进价为80元.若所购进电器均可全部售出,请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com