
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.
【答案】(1)500,![]() ,600,
,600,![]() .(2)小亮选择方式一游泳次数比较多.(3)当
.(2)小亮选择方式一游泳次数比较多.(3)当![]() 时,有
时,有![]() ,小亮选择方式二更合算;当
,小亮选择方式二更合算;当![]() 时,有
时,有![]() ,小亮选择方式一更合算.
,小亮选择方式一更合算.
【解析】
(1)根据两种收费方式填空,并求出函数关系式即可;
(2)将y=2000代入(1)中的函数关系式,求出相应的x的值,即可得到小亮计划拿出2000元用于在此游泳馆游泳,采用哪种付费方式游泳次数比较多;
(3)根据题意,求出两种方式下,x为多少时,收费一样,然后即可得到当x>12时,哪种付费方式更合算.
(1)500,![]() ,600,
,600,![]() .
.
方式一游泳十次:![]() ;
;
方式一游泳x次:![]() ;
;
方式二游泳15次:![]() ;
;
方式二游泳x次:![]() ;
;
(2)方式一:![]() ,解得
,解得![]() .
.
方式二:![]() ,解得
,解得![]() .
.
∵![]() ,
,
∴小亮选择方式一游泳次数比较多.
(3)设方式一与方式二的总费用的差为![]() 元.
元.
则![]() ,即
,即![]() .
.
当![]() 时,即
时,即![]() ,得
,得![]() .
.
∴当![]() 时,小亮选择这两种方式一样合算.
时,小亮选择这两种方式一样合算.
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小.
的增大而减小.
∴当![]() 时,有
时,有![]() ,小亮选择方式二更合算;
,小亮选择方式二更合算;
当![]() 时,有
时,有![]() ,小亮选择方式一更合算.
,小亮选择方式一更合算.


科目:初中数学 来源: 题型:
【题目】马山被誉为“中国民间文化艺术之乡”,马山的民族文化丰富多彩,形式多样.为了了解某学学生对马山民族文化的喜爱情况,某校开展了“我最喜爱的民俗活动”调查问卷,其中包括:![]() 壮族三声部民歌,
壮族三声部民歌,![]() 壮族扁担舞,
壮族扁担舞,![]() 会鼓,
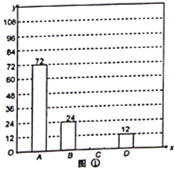
会鼓,![]() 采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
(1)这次抽样调查中,一共抽查了名学生,![]() 项所对应圆心角的度数为;
项所对应圆心角的度数为;
(2)请补全条形统计图;
(3)若九(1)班要从甲、乙、丙和丁这四人中选两个人参与调查,请用列表法或画树状图法求出恰好选中甲乙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(列方程解答)
(2)该车行计划今年新进一批A型车和B型车共60辆,A型车的进货价为每辆1100元,销售价与(1)相同;B型车的进货价为每辆1400元,销售价为每辆2000元,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
![]() ,一次函数
,一次函数![]() ,
,
有下列结论:
①当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
②二次函数![]()
![]() 的图象与
的图象与![]() 轴交点的坐标为
轴交点的坐标为![]() 和
和![]() ;
;
③当![]() 时,
时,![]() ;
;
④在实数范围内,对于![]() 的同一个值,这两个函数所对应的函数值
的同一个值,这两个函数所对应的函数值![]() 均成立,则
均成立,则![]() .
.
其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有![]() 个选项,第二道题有
个选项,第二道题有![]() 个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
(1)如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;
(2)从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为应对新型冠状病毒,某药店老板到厂家选购![]() 、
、![]() 两种品牌的医用外科口罩,
两种品牌的医用外科口罩,![]() 品牌口罩每个进价比
品牌口罩每个进价比![]() 品牌口罩每个进价多0.7元,若用7200元购进
品牌口罩每个进价多0.7元,若用7200元购进![]() 品牌的数量是用5000元购进
品牌的数量是用5000元购进![]() 品牌数量的2倍.
品牌数量的2倍.
(1)求![]() 、
、![]() 两种品牌的口罩每个进价分别为多少元?
两种品牌的口罩每个进价分别为多少元?
(2)若![]() 品牌口罩每个售价为2.1元,
品牌口罩每个售价为2.1元,![]() 品牌口罩每个售价为3元,药店老板决定一次性购进
品牌口罩每个售价为3元,药店老板决定一次性购进![]() 、
、![]() 两种品牌口罩共8000个,在这批口罩全部出售后所获利润不低于3000元.则最少购进
两种品牌口罩共8000个,在这批口罩全部出售后所获利润不低于3000元.则最少购进![]() 品牌口罩多少个?
品牌口罩多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+c(a≠0)的顶点为A(s,t)(其中s≠0).
(1)若抛物线经过(2,7)和(-3,37)两点,且s=1.
①求抛物线的解析式;
②若n>1,设点M(n,y1),N(n+1,y2)在抛物线上,比较y1,y2的大小关系,并说明理由;
(2)若a=2,c=-2,直线y=2x+m与抛物线y=ax2+bx+c的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线y=![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
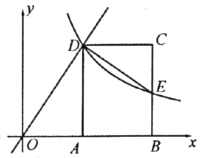
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在直线
在直线![]() 位于第一象限的图像上,反比例函数
位于第一象限的图像上,反比例函数![]() 的图像经过点
的图像经过点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
(1)如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com