Question

10．二次函数图象的顶点在原点O，经过点A（1，$\frac{1}{4}$）；点F（0，1）在y轴上．直线y=-1与y轴交于点H．
（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=-1交于点M，求证：△PFM为等腰三角形；
（3）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=-1交于点M，作PQ⊥FM交FM于点Q，当点P从横坐标2015处运动到横坐标2016处时，请直接写出点Q运动的路径长．

Answer 1

分析 （1）设抛物线的解析式为y=ax²，将点A的坐标代入求得a的值即可；
（2）由两点间的距离公式可求得PM和PF的长，从而得到PM=PF；
（3）由等腰三角形的性质可知点Q是FM的中点，从而得到OQ是△FHM的中位线，由三角形中位线的性质可求得当点P的横坐标为2015时，OQ=1007.5；当点P的横坐标为2016时，OQ=1008，故此可求得点Q运动的路径长．

解答 解：（1）二次函数解析式为：y=ax²，
∵经过点A（1，$\frac{1}{4}$），
∴a=$\frac{1}{4}$，
∴二次函数的解析式y=$\frac{1}{4}$x²．
（2）∵点P是（1）中图象上的点，过点P作x轴的垂线与直线y=-1交于点M，
设P（x，$\frac{1}{4}$x²），则M（x，-1），
∴PM=$\frac{1}{4}$x²+1．
由两点间的距离公式可知：PF=$\sqrt{（x-0）^{2}+（\frac{1}{4}{x}^{2}-1）^{2}}$=$\sqrt{{x}^{2}+\frac{1}{16}{x}^{2}-\frac{1}{2}{x}^{2}+1}$=$\sqrt{\frac{1}{16}{x}^{2}+\frac{1}{2}{x}^{2}+1}$=$\frac{1}{4}{x}^{2}+1$．
∴PF=PM 即△PFM为等腰三角形．
（3）如图所示：过点P作PQ⊥FM，垂足为Q．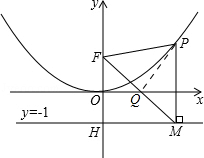

∵PF=PM，PQ⊥FM，
∴FQ=QM．
∵OF=OH，FQ=QM，
∴OQ∥HM，且OQ=$\frac{1}{2}$MH．
当点P的横坐标为2015时，OQ=$\frac{1}{2}$HM=$\frac{1}{2}×2015$=1007.5．
当点P的横坐标为2016时，OQ=$\frac{1}{2}$HM=$\frac{1}{2}×2016$=1008．
∴点Q运动的路径长=1008-1007.5=0.5．

点评 本题主要考查的是二次函数的综合应用、等腰三角形的性质、三角形中位线的性质，证得OQ是△FHM的中位线，利用三角形的中位线的性质求得当点P的横坐标为2015时和当点P的横坐标为2016时OQ的长是解题的关键．