【题目】把下列各数对应的序号填入表示它所在的数集的括号里．
﹣(﹣2.3)，
，0，﹣
，30%，π，﹣|﹣2013|，﹣5
，0.333333…
正数集合{__________________________…}；
负整数集合{________________________…}；
分数集合{__________________________…}；
【答案】（1）正数集合[﹣(﹣2.3)，
，30%，π，0.333333…，…]；（2）负整数集合[﹣
，﹣|﹣2013|，…]；（3）分数集合[﹣(﹣2.3)，，﹣，30%，﹣5
，0.333333…，…]
【解析】
（1）根据小于0的整数是负整数，可得负整数集合；
（2）根据有限小数和无限循环小数是有理数，可得有理数集合，再根据大于0 的有理数是正有理数，可得正有理数集合；
（3）根据整数和分数统称为有理数，可得分数集合．
在﹣(﹣2.3)，，0，﹣，30%，π，﹣|﹣2013|，﹣5，0.333333…中，-（-2.3）=2.3，-|-2013|=-2013，
（1）正数集合[﹣(﹣2.3)，，30%，π，0.333333…，…]
（2）负整数集合[﹣，﹣|﹣2013|，…]
（3）分数集合[﹣(﹣2.3)，，30%，﹣5，0.333333…，…]
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．
（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；
（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；
（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在平面直角坐标系xOy中，抛物线y=ax2﹣2x+c与x轴交于点A和点B（1，0），与y轴相交于点C（0，3）．
（1）求抛物线的解析式和顶点D的坐标；
（2）求证：∠DAB=∠ACB；
（3）点Q在抛物线上，且△ADQ是以AD为底的等腰三角形，求Q点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知
，
两点，且
、
满足
，点
是射线
上的动点（不与
，
重合），将线段
平移到
，使点与点
对应，点
与点
对应，连接
，
.
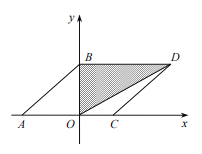
（1）求出点和点的坐标；
（2）设三角形
面积为
，若
，求
的取值范围；
（3）设
，
，
，请给出
，
，
满足的数量关系式，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图（1），数轴上有一个表示数
的点
，已知点在数轴上移动
个单位长度后表示的数是
，那么的值是 ；
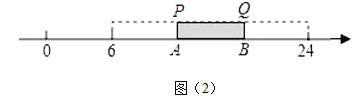
（2）如图（2），有一根木尺
放置在数轴上，它的两端
分别落在
两点处．将木尺在数轴上水平移动，当点
移动到点
时，点
所对应的数为
；当点移动到点
时，点所对应的数为
（单位：
)．利用所学知识求出点、点所表示的数及木尺的长．
（3）借助上面的方法解决问题：一天，小明去问爷爷的年龄，爷爷说：我若是你现在这么大，你还要
年才出生呢，你若是我现在这么大，我已经是
岁！小明纳闷，爷爷今年到底是多少岁？请你画出示意图，求出小明和爷爷的年龄，并写出合理的计算过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，平行四边形OABC的边OA在x轴的正半轴上，A、C两点的坐标分别为（2，0）、（1，2），点B在第一象限，将直线y=-2x沿y轴向上平移m（m＞0）个单位．若平移后的直线与边BC有交点，则m的取值范围是_____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线y=mx2﹣2mx+n（m＜0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴正半轴交于点D，连接AD并延长交x轴于E，连AC、DC．S△DEC：S△AEC=3：4．
（1）求点E的坐标；
（2）△AEC能否为直角三角形？若能，求出此时抛物线的函数表达式；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【问题原型】如图1，在四边形ABCD中，∠ADC=90°，AB=AC.点E、F分别为AC、BC的中点，连结EF，DE．试说明：DE=EF．
【探究】如图2，在问题原型的条件下，当AC平分∠BAD，∠DEF=90°时，求∠BAD的大小．
【应用】如图3，在问题原型的条件下，当AB=2，且四边形CDEF是菱形时，直接写出四边形ABCD的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com