
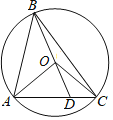
【题目】如图,已知⊙O的半径为1,AB,AC是⊙O的两条弦,且AB=AC,延长BO交AC于点D,连接OA,OC,若AD2=ABDC,则OD=__.
【答案】![]() .
.
【解析】
可证△AOB≌△AOC,推出∠ACO=∠ABD,OA=OC,∠OAC=∠ACO=∠ABD,∠ADO=∠ADB,即可证明△OAD∽△ABD;依据对应边成比例,设OD=x,表示出AB、AD,根据AD2=ABDC,列方程求解即可.
在△AOB和△AOC中,
∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠ABO=∠ACO,
∵OA=OA,
∴∠ACO=∠OAD,
∵∠ADO=∠BDA,
∴△ADO∽△BDA,
∴![]() ,
,
设OD=x,则BD=1+x,
∴![]() ,
,
∴AD![]() ,AB
,AB ,
,
∵DC=AC﹣AD=AB﹣AD,AD2=ABDC,
(![]() )2═
)2═ (
( ),
),
整理得:x2+x﹣1=0,
解得:x![]() 或x
或x![]() (舍去),
(舍去),
因此AD![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
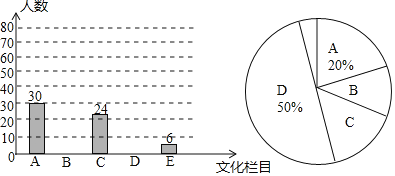
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)将条形统计图补充完整,并求出扇形统计图中“B”所在扇形圆心角的度数;
(3)若选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请用列表法或画树状图的方法求出刚好选到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读):地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图![]() 中的
中的![]() ).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图
).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图![]() 所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角
所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角![]() 的大小是变化的.
的大小是变化的.
(实际应用):观测点![]() 在图1所示的
在图1所示的![]() 上,现在利用这个工具尺在点
上,现在利用这个工具尺在点![]() 处测得
处测得![]() 为
为![]() ,在点
,在点![]() 所在子午线往北的另一个观测点
所在子午线往北的另一个观测点![]() ,用同样的工具尺测得
,用同样的工具尺测得![]() 为
为![]() .
.![]() 是
是![]() 的直径,
的直径,![]() .
.
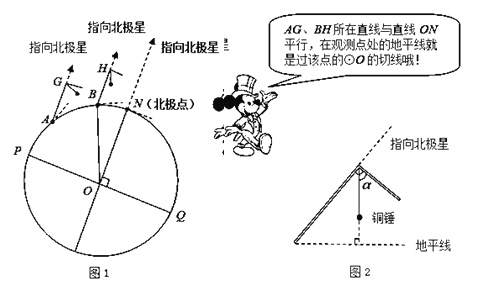
(1)求![]() 的度数;
的度数;
(2)已知![]() km,求这两个观测点之间的距离即
km,求这两个观测点之间的距离即![]() 上
上![]() 的长.(
的长.(![]() 取
取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
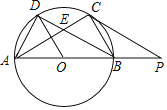
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转得到
顺时针方向旋转得到![]() ,记旋转角为
,记旋转角为![]() ,当
,当![]() 时,作
时,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 交于点
交于点![]()
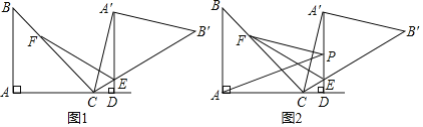
(1)如图1,当![]() 时,作
时,作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.
①写出旋转角![]() 的度数;②求证:
的度数;②求证:![]() ;
;
(2)如图2,在(1)的条件下,设![]() 是直线
是直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,若
,若![]() ,求线段
,求线段![]() 的最小值.(结果保留根号)
的最小值.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去等加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,
若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新特动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC:AB=8cm.DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)点Q在BC上运动时,求t的取值范围;
(2)当点Q在CD上运动时,求t为何值时,△MPQ是等腰三角形;
(3)求S与t之间的函数关系式;当t为何值时,S有最大值?最大值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com