
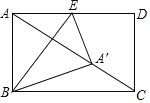
【题目】如图,矩形ABCD中,点E为AD的中点,连结BE,将△ABE沿BE翻折,点A恰好落在AC上的点A处,若AB=2,则AC的长度为_____.
【答案】2![]()
【解析】
连接A'D,设BE与AC交于点M,由翻折知,BE垂直平分AA',证明△ABM≌△CDA',推出A'C=AM,再证明△BAM∽△CAB,设AM=A'M=A'C=x,则AC=3x,通过相似三角形对应边的比相等可求出x的值,进一步求出AC的长度.
解:如图,连接A'D,设BE与AC交于点M,
由翻折知,BE垂直平分AA',
∴AB=A'B=2,AM=A'M,AE=A'E,
∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,∠ABC=90°,
∴∠DCA=∠BAC,
∵点E为AD的中点,
∴AE=DE=A'E,
∴点A,A',D三点在以AD为直径的圆上,
∴∠DA'A=∠DA'C=90°=∠AMB,
∴△ABM≌△CDA'(AAS),
∴A'C=AM,
∴AM=A'M=A'C,
∵∠ABC=∠ANB=90°,∠BAM=∠BAM,
∴△BAM∽△CAB,
∴![]() ,
,
设AM=A'M=A'C=x,则AC=3x,
∴![]() ,
,
解得,x=![]() (取正值),
(取正值),
∴3x=2![]() ,
,
∴AC=2![]() ,
,
故答案为:2![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
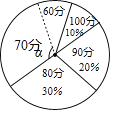
【题目】某校有20名同学参加市举办的“文明环保,从我做起”征文比赛,成绩分别记为60分、70分、80分、90分、100分,为方便奖励,现统计出80分、90分、100分的人数,制成如图不完整的扇形统计图,设70分所对扇形圆心角为α.
(1)若从这20份征文中,随机抽取一份,则抽到试卷的分数为低于80分的概率是 ;
(2)当![]() 时,求成绩是60分的人数;
时,求成绩是60分的人数;
(3)设80分为唯一众数,求这20名同学的平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是______.
(2)如果小明将“求助”留在第二题使用,那么小明顺利通关的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.
(1)求证:CF⊥AE;
(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为M,连接CF,若CG=GM.
①求证:CF=CM;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
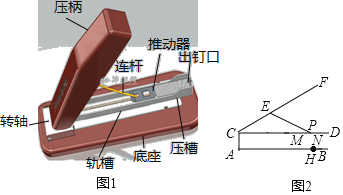
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com