
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.
(1)求证:CF⊥AE;
(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为M,连接CF,若CG=GM.
①求证:CF=CM;
②求![]() 的值.
的值.
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
![]() 证明
证明![]() ≌
≌![]() ,结合直角三角形斜边中线的性质解决问题即可.
,结合直角三角形斜边中线的性质解决问题即可.
![]() 证明四边形CDFM是平行四边形,即可解决问题.
证明四边形CDFM是平行四边形,即可解决问题.
![]() 连接EF,
连接EF,![]() 设
设![]() ,证明
,证明![]() ,把问题转化为:
,把问题转化为:![]() ,求出OG,
,求出OG,![]() 用a表示
用a表示![]() ,即可解决问题.
,即可解决问题.
(1)证明:如图1中,
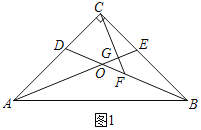
∵AC=BC,∠ACE=∠BCD=90°,CE=CD,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵DF=FB,
∴CF=FD=FB,
∴∠FCB=∠FBC,
∴∠FCB=∠CAB,
∵∠CAB+∠AEC=90°,
∴∠AEC+∠FCB=90°,
∴∠CGE=90°,
∴CF⊥AE.
(2)①证明:如图2中,
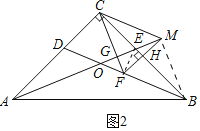
∵FM⊥BC,
∴∠FHC=∠CGE=∠MGF=90°,
∴∠ECG+∠CEG=90°,∠ECG+∠CFH=90°,
∴∠CEG=∠CFH,
∴CG=GM,
∴△CGE≌△MGF(AAS),
∴CE=FM,EG=GF,
∵CD=CE,
∴CD=FM,
∵∠FHB=∠ACB=90°,
∴CD∥FM,
∴四边形CDFM是平行四边形,
∴CM=DF,
∵CF=DF=FB,
∴CM=CF.
②连接EF,BM.设FG=EG=a,
∵CM=BF,CM∥BF,
∴FG∥BM,
∴![]() =
=![]() ,
,
∵△CAE≌△CBD,
∴∠CAE=∠CBD,∵∠CAB=∠CBA,
∴∠OAB=∠OBA,
∴OA=OB,
∴![]() =
=![]() ,
,
易知OG=GF=EG=a,EF=EM=![]() a,
a,
∴OM=2a+![]() a,
a,
∴![]() =
=![]() =
=![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
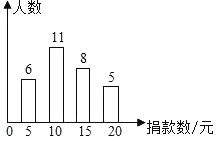
(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
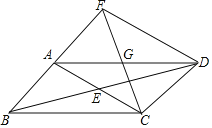
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③![]() ;④(a﹣b)2S△EFO=b2S△DGO.其中结论正确的个数是( )
;④(a﹣b)2S△EFO=b2S△DGO.其中结论正确的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点P是直线AC上一点,将△ADP沿DP所在的直线翻折后,点A落在A1处,若A1D⊥AC,则点P与点A之间的距离为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.
(1)当10≤x<60时,求y关于x的函数表达式;
(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;
①若两次购买鞋子共花费9200元,求第一次的购买数量;
②如何规划两次购买的方案,使所花费用最少,最少多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
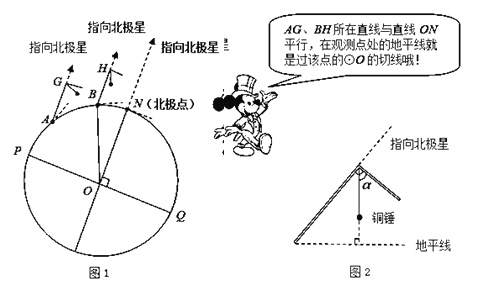
【题目】(材料阅读):地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图![]() 中的
中的![]() ).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图
).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图![]() 所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角
所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角![]() 的大小是变化的.
的大小是变化的.
(实际应用):观测点![]() 在图1所示的
在图1所示的![]() 上,现在利用这个工具尺在点
上,现在利用这个工具尺在点![]() 处测得
处测得![]() 为
为![]() ,在点
,在点![]() 所在子午线往北的另一个观测点
所在子午线往北的另一个观测点![]() ,用同样的工具尺测得
,用同样的工具尺测得![]() 为
为![]() .
.![]() 是
是![]() 的直径,
的直径,![]() .
.
(1)求![]() 的度数;
的度数;
(2)已知![]() km,求这两个观测点之间的距离即
km,求这两个观测点之间的距离即![]() 上
上![]() 的长.(
的长.(![]() 取
取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
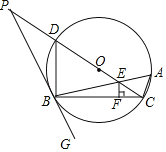
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com