
ЁОЬтФПЁПСЂЖЈЬјдЖЪЧМЮаЫЪаЬхг§жаПМЕФГщПМЯюФПжЎвЛЃЌФГаЃОХФъМЖЃЈ1ЃЉЃЌЃЈ2ЃЉАрзМБИМЏЬхЙКТђФГЦЗХЦЕФСЂЖЈЬјдЖбЕСЗаЌЃЎЯжСЫНтЕНФГЭјЕъе§КУгаетжжЦЗХЦбЕСЗаЌЕФДйЯњЛюЖЏЃЌЦфЙКТђЕФЕЅМлyЃЈдЊ/ЫЋЃЉгывЛДЮадЙКТђЕФЪ§СПxЃЈЫЋЃЉжЎМфТњзуЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЕБ10ЁмxЃМ60ЪБЃЌЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉОХЃЈ1ЃЉЃЌЃЈ2ЃЉАрЙВЙКТђДЫЦЗХЦаЌзг100ЫЋЃЌгЩгкФГжждвђашЗжСНДЮЙКТђЃЌЧввЛДЮЙКТђЪ§СПЖргк25ЫЋЧвЩйгк60ЫЋЃЛ
ЂйШєСНДЮЙКТђаЌзгЙВЛЈЗб9200дЊЃЌЧѓЕквЛДЮЕФЙКТђЪ§СПЃЛ
ЂкШчКЮЙцЛЎСНДЮЙКТђЕФЗНАИЃЌЪЙЫљЛЈЗбгУзюЩйЃЌзюЩйЖрЩйдЊЃП

ЁОД№АИЁПЃЈ1ЃЉyЃН150ЉxЃЛ ЃЈ2ЃЉЂйЕквЛХњЙКТђЪ§СПЮЊ30ЫЋЛђ40ЫЋЃЎЂкЕквЛДЮТђ26ЫЋЃЌЕкЖўДЮТђ74ЫЋзюЪЁЧЎЃЌзюЩй9144дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШєЙКТђxЫЋЃЈ10ЃМxЃМ60ЃЉЃЌУПМўЕФЕЅМлЃН140ЉЃЈЙКТђЪ§СПЉ10ЃЉЃЌвРДЫПЩЕУyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЂйЩшЕквЛХњЙКТђxЫЋЃЌдђЕкЖўХњЙКТђЃЈ100ЉxЃЉЫЋЃЌИљОнЙКТђСНХњаЌзгвЛЙВЛЈСЫ9200дЊСаГіЗНГЬЧѓНтМДПЩЃЎЗжСНжжЧщПіПМТЧЃКЕБ25ЃМxЁм40ЪБЃЌдђ60Ём100ЉxЃМ75ЃЛЕБ40ЃМxЃМ60ЪБЃЌдђ40ЃМ100ЉxЃМ60ЃЎ
ЂкАбСНДЮЕФЛЈЗбгыЕквЛДЮЙКТђЕФЫЋЪ§гУКЏЪ§БэЪОГіРДЃЎ
НтЃКЃЈ1ЃЉЙКТђxЫЋЃЈ10ЃМxЃМ60ЃЉЪБЃЌyЃН140ЉЃЈxЉ10ЃЉЃН150ЉxЃЎ
ЙЪyЙигкxЕФКЏЪ§ЙиЯЕЪНЪЧyЃН150ЉxЃЛ
ЃЈ2ЃЉЂйЩшЕквЛХњЙКТђxЫЋЃЌдђЕкЖўХњЙКТђЃЈ100ЉxЃЉЫЋЃЎ
ЕБ25ЃМxЁм40ЪБЃЌдђ60Ём100ЉxЃМ75ЃЌдђxЃЈ150ЉxЃЉ+80ЃЈ100ЉxЃЉЃН9200ЃЌ
НтЕУx1ЃН30ЃЌx2ЃН40ЃЛ
ЕБ40ЃМxЃМ60ЪБЃЌдђ40ЃМ100ЉxЃМ60ЃЌ
дђxЃЈ150ЉxЃЉ+ЃЈ100ЉxЃЉ[150ЉЃЈ100ЉxЃЉ]ЃН9200ЃЌ
НтЕУxЃН30ЛђxЃН70ЃЌЕЋ40ЃМxЃМ60ЃЌЫљвдЮоНтЃЛ
Д№ЃКЕквЛХњЙКТђЪ§СПЮЊ30ЫЋЛђ40ЫЋЃЎ
ЂкЩшЕквЛДЮЙКТђxЫЋЃЌдђЕкЖўДЮЙКТђЃЈ100ЉxЃЉЫЋЃЌЩшСНДЮЛЈЗбwдЊЃЎ
ЕБ25ЃМxЁм40ЪБwЃНxЃЈ150ЉxЃЉ+80ЃЈ100ЉxЃЉЃНЉЃЈxЉ35ЃЉ2+9225ЃЌ
ЁрxЃН26ЪБЃЌwгазюаЁжЕЃЌзюаЁжЕЮЊ9144дЊЃЛ
ЕБ40ЃМxЃМ60ЪБЃЌ
wЃНxЃЈ150ЉxЃЉ+ЃЈ100ЉxЃЉ[150ЉЃЈ100ЉxЃЉ]ЃНЉ2ЃЈxЉ50ЃЉ2+10000ЃЌ
ЁрxЃН41Лђ59ЪБЃЌwгазюаЁжЕЃЌзюаЁжЕЮЊ9838дЊЃЌ
злЩЯЫљЪіЃКЕквЛДЮТђ26ЫЋЃЌЕкЖўДЮТђ74ЫЋзюЪЁЧЎЃЌзюЩй9144дЊЃЎ


 ХргХПкЫуЬтПЈЯЕСаД№АИ
ХргХПкЫуЬтПЈЯЕСаД№АИ ПЊаФПкЫуЬтПЈЯЕСаД№АИ
ПЊаФПкЫуЬтПЈЯЕСаД№АИ ПкЫуЬтПЈКгББЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈКгББЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ AМгН№Ьт ЯЕСаД№АИ
AМгН№Ьт ЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЦјЯѓОжЭГМЦСЫ5дТ1ШежС8ШежаЮч12ЪБЕФЦјЮТ(ЕЅЮЛ![]() )ЃЌећРэКѓЗжБ№ЛцжЦГЩШчЭМЫљЪОЕФСНЗљЭГМЦЭМЃЎ
)ЃЌећРэКѓЗжБ№ЛцжЦГЩШчЭМЫљЪОЕФСНЗљЭГМЦЭМЃЎ
ИљОнЭМжаИјГіЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК

(1)ИУЪа5дТ1ШежС8ШежаЮчЪБЦјЮТЕФЦНОљЪ§ЪЧЁЁ ![]() ЃЌжаЮЛЪ§ЪЧЁЁ
ЃЌжаЮЛЪ§ЪЧЁЁ ![]() ЃЛ
ЃЛ
(2)ЧѓЩШаЮЭГМЦЭМжаЩШаЮ![]() ЕФдВаФНЧЕФЖШЪ§ЃЛ
ЕФдВаФНЧЕФЖШЪ§ЃЛ
(3)ЯжДгИУЪа5дТ1ШежС5ШеЕФ![]() ЬьжаЃЌЫцЛњГщШЁ
ЬьжаЃЌЫцЛњГщШЁ![]() ЬьЃЌЧѓЧЁКУГщЕН
ЬьЃЌЧѓЧЁКУГщЕН![]() ЬьжаЮч12ЪБЕФЦјЮТОљЕЭгк
ЬьжаЮч12ЪБЕФЦјЮТОљЕЭгк![]()
![]() ЕФИХТЪЃЎ
ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
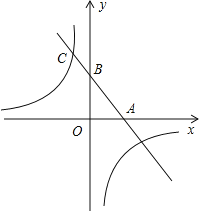
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓгыxжсЃЌyжсЗжБ№ЯрНЛгкAЃЌBСНЕуЃЌЧвгыЗДБШР§КЏЪ§yЃНЉ![]() ЕФЭМЯѓдкЕкЖўЯѓЯоНЛгыЕуCЃЌШчЙћЕуAЮЊЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌBЪЧACЕФжаЕуЃЎ
ЕФЭМЯѓдкЕкЖўЯѓЯоНЛгыЕуCЃЌШчЙћЕуAЮЊЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌBЪЧACЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓЕуCЕФзјБъМАkЁЂbЕФжЕЃЎ
ЃЈ2ЃЉЧѓГівЛДЮКЏЪ§ЭМЯѓгыЗДБШР§КЏЪ§ЭМЯѓЕФСэвЛИіНЛЕуЕФзјБъЃЌВЂжБНгаДГіЕБ![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌAC=BCЃЌЁЯACB=90ЁуЃЌЕуDЁЂEЗжБ№дкACЁЂBCЩЯЃЌBDгыAEНЛгкЕуOЃЌЧвCD=CEЃЌШєЕуFЪЧBDЕФжаЕуЃЌСЌНгCFЃЌНЛAEгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКCFЁЭAEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуFзїFMЁЭBCЃЌНЛAEЕФбгГЄЯпгкЕуMЃЌДЙзуЮЊMЃЌСЌНгCFЃЌШєCG=GMЃЎ
ЂйЧѓжЄЃКCF=CMЃЛ
ЂкЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
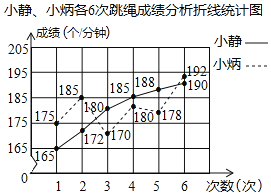
ЁОЬтФПЁПЬхг§РЯЪІвЊДгУПАрбЁШЁвЛУћЭЌбЇЃЌВЮМгбЇаЃЕФЬјЩўБШШќЃЎаЁОВКЭаЁБўЪЧЬјЩўФмЪжЃЌЯТУцЗжБ№ЪЧаЁОВЁЂаЁБўИї6ДЮЬјЩўГЩМЈЭГМЦЭМКЭГЩМЈЗжЮіБэ
аЁОВЁЂаЁБўИї6ДЮЬјЩўГЩМЈЗжЮіБэ
ГЩМЈ аеУћ | ЦНОљЪ§ | жаЮЛЪ§ | ЗНВю |
аЁОВ | 180 | 182.5 | 79.7 |
аЁБў | 180 | a | 33 |
ЃЈ1ЃЉИљОнЭГМЦЭМЕФЪ§ОнЃЌМЦЫуГЩМЈЗжЮіБэжаaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉНсКЯвдЩЯаХЯЂЃЌЧыФуДгСНИіВЛЭЌНЧЖШЦРМлетСНЮЛбЇЩњЕФЬјЩўЫЎЦНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌЙ§дЕуOМАЕуAЃЈ8ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉзїОиаЮOABCЁЂСЌНсOBЃЌЕуDЮЊOBЕФжаЕуЃЌЕуEЪЧЯпЖЮABЩЯЕФЖЏЕуЃЌСЌНсDEЃЌзїDFЁЭDEЃЌНЛOAгкЕуFЃЌСЌНсEFЃЎвбжЊЕуEДгAЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдкЯпЖЮABЩЯвЦЖЏЃЌЩшвЦЖЏЪБМфЮЊtУыЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБt=3ЪБЃЌЧѓDFЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкЯпЖЮABЩЯвЦЖЏЕФЙ§ГЬжаЃЌЁЯDEFЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛБфЃЌЧыЧѓГіtanЁЯDEFЕФжЕЃЎ
ЃЈ3ЃЉСЌНсADЃЌЕБADНЋЁїDEFЗжГЩЕФСНВПЗжЕФУцЛ§жЎБШЮЊ1ЃК2ЪБЃЌЧѓЯргІЕФtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЕу![]() ЮЊЖўДЮКЏЪ§
ЮЊЖўДЮКЏЪ§![]() ЭМЯѓЕФЖЅЕуЃЌжБЯп
ЭМЯѓЕФЖЅЕуЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсе§АыжсЃЌ
жсе§АыжсЃЌ![]() жсгкЕу
жсгкЕу![]() .
.
ЃЈ1ЃЉШчЭМ1ЃЌШєЖўДЮКЏЪ§ЭМЯѓвВОЙ§Еу![]() ЃЌЪдЧѓГіИУЖўДЮКЏЪ§НтЮіЪНЃЌВЂЧѓГі
ЃЌЪдЧѓГіИУЖўДЮКЏЪ§НтЮіЪНЃЌВЂЧѓГі![]() ЕФжЕ.
ЕФжЕ.
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ФкЃЌШєЕу
ФкЃЌШєЕу![]() ЃЌ
ЃЌ![]() ЖМдкЖўДЮКЏЪ§ЭМЯѓЩЯЃЌЪдБШНЯ
ЖМдкЖўДЮКЏЪ§ЭМЯѓЩЯЃЌЪдБШНЯ![]() гы
гы![]() ЕФДѓаЁ.
ЕФДѓаЁ.
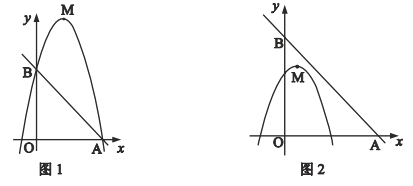
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧе§ЗНаЮ
ЪЧе§ЗНаЮ![]() ЕФБп
ЕФБп![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() гы
гы![]() Йигк
Йигк![]() ЖдГЦЃЌ
ЖдГЦЃЌ![]() ЕФбгГЄЯпгы
ЕФбгГЄЯпгы![]() НЛгкЕу
НЛгкЕу![]() ЃЌгы
ЃЌгы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌзїе§ЗНаЮ
ЕФбгГЄЯпЩЯЃЌзїе§ЗНаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌМЧе§ЗНаЮ
ЃЌМЧе§ЗНаЮ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЗжБ№ЮЊ
ЕФУцЛ§ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
ЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
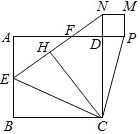
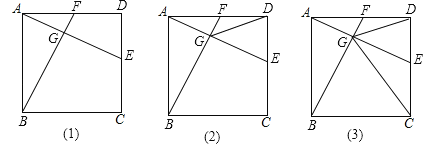
ЁОЬтФПЁПШчЭМЃЈ1ЃЉдке§ЗНаЮABCDжаЃЌЕуEЪЧCDБпЩЯвЛЖЏЕуЃЌСЌНгAEЃЌзїBFЁЭAEЃЌДЙзуЮЊGНЛADгкF
ЃЈ1ЃЉЧѓжЄЃКAFЃНDEЃЛ
ЃЈ2ЃЉСЌНгDGЃЌШєDGЦНЗжЁЯEGFЃЌШчЭМЃЈ2ЃЉЃЌЧѓжЄЃКЕуEЪЧCDжаЕуЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгCGЃЌШчЭМЃЈ3ЃЉЃЌЧѓжЄЃКCGЃНCDЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com