
【题目】已知:如图,在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线交边
的垂线交边![]() 于点
于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() .
.
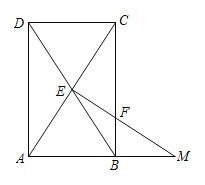
求证:(1)四边形![]() 是矩形;
是矩形;
(2)![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由![]() 可得
可得![]() ,又∠CAB=∠EAM,从而推出△ABC∽△AEM,继而推出∠ABC=∠AEM=90°,从而可得出结论;
,又∠CAB=∠EAM,从而推出△ABC∽△AEM,继而推出∠ABC=∠AEM=90°,从而可得出结论;
(2)先证明△EFB∽△EBM,从而推出![]() ,得出
,得出![]() ,又DE=BE,从而可得出结果.
,又DE=BE,从而可得出结果.
证明:(1)∵![]() ,∴
,∴![]() ,
,
又∠CAB=∠EAM,
∴△ABC∽△AEM,
∴∠ABC=∠AEM=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;
(2)∵四边形ABCD为矩形,∴AE=BE=DE=CE,
∴∠EAB=∠EBA,又∠EAB+∠M=90°,∠EBA+∠EBF=90°
∴∠M=∠EBF,
又∠FEB=∠BEM,
∴△EFB∽△EBM,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
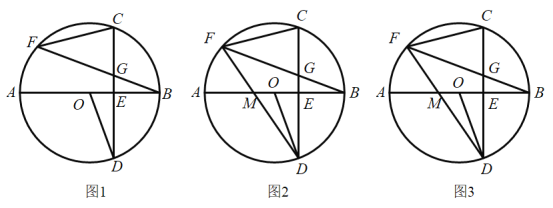
(1)求证:![]() ;
;
(2)如图2,连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() 是等腰三角形;
是等腰三角形;
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目.为了了解全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中一个项目),并把调查结果绘制成如图所示的统计图,根据这个统计图可以估计该学校1500名学生中选择篮球项目的学生约为______名.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E为射线CB上一动点(不与点C重合),将△CDE沿DE所在直线折叠,点C落在点C′处,连接AC′,当△AC′D为直角三角形时,CE的长为_____.
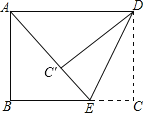
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)定义:如图1,点E在四边形ABCD的边CD上,若AE、BE将四边形ABCD分割成三个相似的三角形,则称点E为该四边形的相似点.

(1)若相似点在四边形ABCD的边CD上, 且AE、BE将四边形ABCD分割成三个正三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(2)若相似点在四边形ABCD的边CD上,且AE、BE将四边形ABCD分割成三个全等的等腰直角三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(3)(探索研究)
如图2,点E为四边形ABCD边上的相似点,且AE、BE将四边形ABCD分割成三个全等的三角形,已知∠ABC=90°,AD=AB=BC=2,求边CD的长.
(4)(问题解决)
如图3,在四边形ABCD中,AB∥CD,点E为四边形ABCD的边CD上的相似点,且AD=a,AB=b,BC=c(其中a≠c),此时边CD的长为多少?请用含a、b、c的代数式直接写出所有可能的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com