
【题目】已知a,b,c为非零的实数,则![]() 的可能值的个数为( )
的可能值的个数为( )
A. 4 B. 5 C. 6 D. 7
【答案】A
【解析】分a、b、c三个数都是正数,两个正数,一个正数,都是负数四种情况,根据绝对值的性质去掉绝对值号,再根据有理数的加法运算法则进行计算即可得解.
①a、b、c三个数都是正数时,a>0,ab>0,ac>0,bc>0,
原式=1+1+1+1
=4;
②a、b、c中有两个正数时,
设为a>0,b>0,c<0,
则ab>0,ac<0,bc<0,
原式=1+1-1-1
=0;
设为a>0,b<0,c>0,
则ab<0,ac>0,bc<0,
原式=1-1+1-1
=0;
设为a<0,b>0,c>0,
则ab<0,ac<0,bc>0,
原式=-1-1-1+1
=-2;
③a、b、c有一个正数时,
设为a>0,b<0,c<0,
则ab<0,ac<0,bc>0,
原式=1-1-1+1
=0;
设为a<0,b>0,c<0,
则ab<0,ac>0,bc<0,
原式=-1-1+1-1
=-2;
设为a<0,b<0,c>0,
则ab>0,ac<0,bc<0,
原式=-1+1-1-1
=-2;
④a、b、c三个数都是负数时,即a<0,b<0,c<0,
则ab>0,ac>0,bc>0,
原式=-1+1+1+1
=2.
综上所述,![]() 的可能值的个数为4.
的可能值的个数为4.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )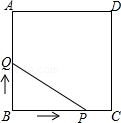
A.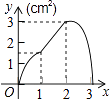
B.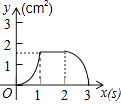
C.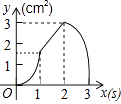
D.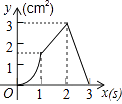
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
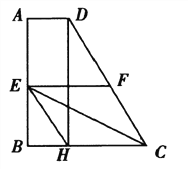
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, O为正方形ABCD的中心,分别延长OA,OD到点F,E,使OF=2OA,OE=2OD,连接EF,将△FOE绕点O按逆时针方向旋转角α得到△FOE,连接AE,BF(如图2).
(1)探究AE与BF的数量关系,并给予证明;
(2)当α=30°时,求证: △AOE为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com