
【题目】如图1, O为正方形ABCD的中心,分别延长OA,OD到点F,E,使OF=2OA,OE=2OD,连接EF,将△FOE绕点O按逆时针方向旋转角α得到△FOE,连接AE,BF(如图2).
(1)探究AE与BF的数量关系,并给予证明;
(2)当α=30°时,求证: △AOE为直角三角形.

【答案】(1)AE=BF,理由见解析;(2)证明见解析.
【解析】试题分析:(1)利用旋转不变量找到相等的角和线段,证得△E′AO≌△F′BO后即可证得结论;
(2)利用已知角,得出∠GAE′=∠GE′A=30°,从而证明直角三角形.
试题解析:(1)证明:∵O为正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E′OF′,
∴OE′=OF′,
∵∠F′OB=∠E′OA,OA=OB,
在△E′AO和△F′BO中,
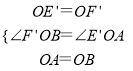 ,
,
∴△E′AO≌△F′BO,
∴AE′=BF′;
(2)证明:∵取OE′中点G,连接AG,
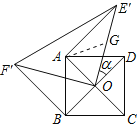
∵∠AOD=90°,α=30°,
∴∠E′OA=90°-α=60°,
∵OE′=2OA,
∴OA=OG,
∴∠E′OA=∠AGO=∠OAG=60°,
∴AG=GE′,
∴∠GAE′=∠GE′A=30°,
∴∠E′AO=90°,
∴△AOE′为直角三角形.


科目:初中数学 来源: 题型:
【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |

(1)频数分布表中的m= , n=;
(2)样本中位数所在成绩的级别是 , 扇形统计图中,E组所对应的扇形圆心角的度数是;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分类
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整数:{ …}
(2)负整数:{ …}
(3)整数:{ …}
(4)分数:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中, ①AE和BF的位置关系为;
②线段MN的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简 [x]+(x)+[x)的结果是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
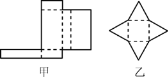
【题目】观察图,回答下列问题:
(1)甲、乙两图分别能折成什么几何体?简述它们的特征;
(2)设几何体的面数为F,顶点数为V,棱数为E,请计算(1)中两个几何体的F+V-E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.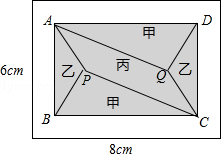
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com