
【题目】学校捐资购买了一批物资120吨打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载):
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车来运送,需运费8200元,则分别需甲、乙两种车各几辆?
(2)为了节省运费,该公司打算用甲、乙、丙三种车同时参与运送,已知它们的总辆数为14辆,请你分别求出三种车的辆数,并求出此时的运费.
【答案】(1)需甲种车8辆,乙种车10辆;(2)甲种车有2辆,乙种车有5辆,丙种车有7辆,此时的运费是7500元.
【解析】
(1)设需甲车x辆,乙车y辆列出方程组即可;
(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,列出等式.
(1)设需甲种车x辆,乙种车y辆.
根据题意,得![]() ,
,
解得![]() ,
,
答:需甲种车8辆,乙种车10辆;
(2)设甲种车有a辆,乙种车有b辆,则丙种车有(14-a-b)辆,
由题意得5a+8b+10(14-a-b)=120,
化简得5a+2b=20,
即a=4-![]() b,
b,
因为a,b,14-a-b均为正整数,
所以b只能等于5,从而a=2,14-a-b=7,
所以甲种车有2辆,乙种车有5辆,丙种车有7辆,
所以需运费400×2+500×5+600×7=7500(元).
答:甲种车有2辆,乙种车有5辆,丙种车有7辆,此时的运费是7500元.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
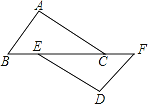
【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.
(1)求证:AB=DF;
(2)若BC=9,EC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x名工人生产螺钉,依题意列方程为( )
A. 1200x=2000(22-x) B. 1200x=2![]() 2000(22-x)
2000(22-x)
C. 1200(22-x)=2000x D. 2![]() 1200x=2000(22-x)
1200x=2000(22-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d= ![]() 计算. 例如:求点P(﹣1,2)到直线y=3x+7的距离.
计算. 例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为d= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)点P(1,﹣1)到直线y=x+1的距离;
(2)已知⊙Q的圆心Q的坐标为(0,4),半径r为2,判断⊙Q与直线y= ![]() x+8的位置关系并说明理由;
x+8的位置关系并说明理由;
(3)已知直线y=﹣2x+1与y=﹣2x+6平行,A、B是直线y=﹣2x+1上的两点且AB=8,P是直线y=﹣2x+6上任意一点,求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
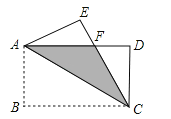
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
方案①:甲队单独完成此项工程刚好如期完工;
方案②:乙队单独完成此项工程要比规定工期多用5天;
方案③:若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
(1)求甲、乙两队单独完成此项工程各需多少天?
(2)如果工程不能如期完工,公司每天将损失3000元,如果你是公司经理,你觉得哪一种施工方案划算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发.不久,第二列快车也从甲地发往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分后,第二列快车与慢车相遇.设慢车行驶的时间为x(单位:时),慢车与第一、第二列快车之间的距离y(单位:千米)与x(单位:时)之间的函数关系如图1、图2, 
根据图象信息解答下列问题:
(1)甲、乙两地之间的距离为千米.
(2)求图1中线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接在图2中的( )内填上正确的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com