
����Ŀ����֪��P��x0 �� y0����ֱ��y=kx+b�����P��ֱ��y=kx+b�ľ���d���ù�ʽd= ![]() ���㣮 ���磺���P����1��2����ֱ��y=3x+7�ľ��룮
���㣮 ���磺���P����1��2����ֱ��y=3x+7�ľ��룮
�⣺��Ϊֱ��y=3x+7������k=3��b=7��
���Ե�P����1��2����ֱ��y=3x+7�ľ���Ϊd= ![]() =
= ![]() =
= ![]() ��
��
�������ϲ��ϣ�����������⣺
��1����P��1����1����ֱ��y=x+1�ľ��룻
��2����֪��Q��Բ��Q������Ϊ��0��4�����뾶rΪ2���жϡ�Q��ֱ��y= ![]() x+8��λ�ù�ϵ��˵�����ɣ�
x+8��λ�ù�ϵ��˵�����ɣ�
��3����ֱ֪��y=��2x+1��y=��2x+6ƽ�У�A��B��ֱ��y=��2x+1�ϵ�������AB=8��P��ֱ��y=��2x+6������һ�㣬���PAB�������
���𰸡�
��1���⣺���ݵ㵽ֱ�ߵľ��빫ʽ��֪����P��1����1����ֱ��y=x+1�ľ���d= ![]() =
= ![]()
��2���⣺���ۣ��жϡ�Q��ֱ��y= ![]() x+8���У�
x+8����
���ɣ����ݵ㵽ֱ�ߵľ��빫ʽ��֪����Q��0��4����ֱ��y= ![]() x+8�ľ���d=
x+8�ľ���d= ![]() =2��
=2��
�ߡ�Q�İ뾶Ϊ2��
��d=r��
���Q��ֱ��y= ![]() x+8����
x+8����
��3���⣺��ֱ��y=��2x+6��ȡһ��Q��0��6����
���ݵ㵽ֱ�ߵľ��빫ʽ��֪����Q��0��6������ֱ��y=��2x+1�ľ���d= ![]() =
= ![]() ��
��
��ֱ��y=��2x+1��y=��2x+6ƽ�У�
��S��PAB= ![]() ABd=
ABd= ![]() 8
8 ![]() =4
=4 ![]()
����������1�����ݵ㵽ֱ�ߵľ��빫ʽ���㼴�ɣ���2�������Q��0��4����ֱ��y= ![]() x+8�ľ���d�����жϣ���3����ֱ��y=��2x+6��ȡһ��Q��0��6�������ݵ㵽ֱ�ߵľ��빫ʽ��֪����Q��0��6������ֱ��y=��2x+1�ľ���d=
x+8�ľ���d�����жϣ���3����ֱ��y=��2x+6��ȡһ��Q��0��6�������ݵ㵽ֱ�ߵľ��빫ʽ��֪����Q��0��6������ֱ��y=��2x+1�ľ���d= ![]() ������ƽ���ߵ����ʼ��ɽ�����⣻
������ƽ���ߵ����ʼ��ɽ�����⣻


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����ABΪֱ���ġ�O�ֱ�AC��D��BC��E������ED����ED=EC�� 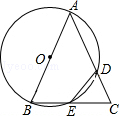
��1����֤��AB=AC��
��2����AB=4��BC=2 ![]() ����CD�ij���
����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
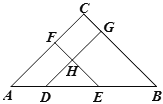
����Ŀ����ͼ���ڡ�ABC�� ����A=��B��D��E�DZ�AB�ϵĵ㣬DG��AC��EF��BC��DG��EF�� ���ڵ�H��
(1)��HDE���HED�Ƿ���ȣ���˵�����ɣ�
��:��HDE=��HED���������£�
��DG��AC(��֪)
���� �������� ���� �� ���� ���� ������
�� EF��BC (��֪)
������ ������ ���� �� �� ����
�֡ߡ�A=��B (��֪)
�� �� �� ��.
(2)�����C=90�㣬DG�� EF�к�λ�ù�ϵ�������� (1)�еĽ��˵�����ɣ�
�⣺�������������������������£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����m�Ǵө�1��0��1��2�ĸ�������ȡ��һ������n�Ǵө�2��0��3����������ȡ��һ����������κ���y=��x��m��2+n�Ķ������������ϵĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
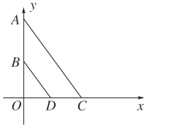
����Ŀ����ͼ8����ƽ��ֱ������ϵxOy�У�A(0��8)��B(0��4)����C��x����������ϣ���DΪOC���е㣮
��1����BD��AC�ľ������2ʱ�����߶�OC�ij���
��2�����OE��AC�ڵ�E�����ı���ABDEΪƽ���ı���ʱ����ֱ��BD�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=ax2+bx+c��a��0������ԭ�㣬����ΪA��s��t����s��0���� 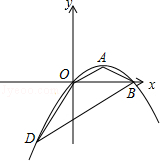
��1����s=2ʱ��t=1ʱ���������߶�Ӧ�Ķ��κ����ı���ʽ��
��2������1���е���������x�ύ�ڵ�B����B��OA��ƽ���߽��������ڵ�D�����BDO�����ߵĺͣ�
��3������A��������y=x2��x�ϣ��ҩ�1��s��2ʱ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ���ʹ�����һ������120�ִ���֧Ԯɽ�������мס��ҡ������ֳ���ѡ��ÿ�����������������˷����±���ʾ(����ÿ����������)��
���� | �� | �� | �� |
����������(��/��) | 5 | 8 | 10 |
�����˷�(Ԫ/��) | 400 | 500 | 600 |
(1)��ȫ�����ʶ��üס������ֳ������ͣ����˷�8200Ԫ����ֱ���ס������ֳ���������
(2)Ϊ�˽�ʡ�˷ѣ��ù�˾�����üס��ҡ������ֳ�ͬʱ�������ͣ���֪���ǵ�������Ϊ14��������ֱ�������ֳ����������������ʱ���˷ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC��EF��ֱƽ��AC����AC�ڵ�F����BC�ڵ�E����BD=DE��
������BAE=40�������C�Ķ�����
������ABC�ܳ�13cm��AC=6cm����DC����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com