
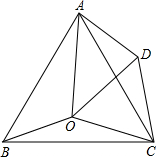
 如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.
如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.分析 (1)如图,根据等边三角形的性质得∠ACB=60°,CA=CB,∠OCD=∠3=∠4=60°,OC=CD,则利用旋转的定义,把△BCO绕点C顺时针旋转60°可得到△ACD,再根据旋转的性质得∠ADC=∠BOC=α,于是可计算出∠2=∠ADC-∠4=90°,∠1=360°-150°-60°-110°=40°,所以△AOD为直角三角形;
(2)由(1)可得∠2=∠ADC-∠4=α-60°,∠1=360°-α-60°-110°=190°-α,则利用三角形内角和定理可得∠OAD=180°-∠1-∠2=50°;
(3)分类讨论:当∠1=∠2时,△AOD是等腰三角形,则α-60°=190°-α;当∠2=∠OAD时,△AOD是等腰三角形,则α-60°=50°;当∠1=∠OAD时,△AOD是等腰三角形,则190°-α=50°,然后分别解方程即可得到α的值.
解答 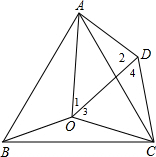 解:(1)△AOD为直角三角形.理由如下:
解:(1)△AOD为直角三角形.理由如下:
如图,∵△ABC和△COD都是等边三角形,
∴∠ACB=60°,CA=CB,∠OCD=∠3=∠4=60°,OC=CD,
∴△BCO绕点C顺时针旋转60°可得到△ACD,
∴∠ADC=∠BOC=α,
∵α=150°,
∴∠2=∠ADC-∠4=150°-60°=90°,∠1=360°-150°-60°-110°=40°,
∴△AOD为直角三角形;
(2)∵∠2=∠ADC-∠4=α-60°,∠1=360°-α-60°-110°=190°-α,
∴∠OAD=180°-∠1-∠2=180°-(α-60°)-(190°-α)=50°;
(3)当∠1=∠2时,△AOD是等腰三角形,则α-60°=190°-α,解得α=125°;
当∠2=∠OAD时,△AOD是等腰三角形,则α-60°=50°,解得α=110°;
当∠1=∠OAD时,△AOD是等腰三角形,则190°-α=50°,解得α=140°,
综上所述,当α为110°或125°或140°时,△AOD是等腰三角形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的判定和等边三角形的判定与性质.注意分类讨论思想的运用.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 对应点到旋转中心的距离相等 | B. | 图形上每一部分旋转的角度相同 | ||
| C. | 旋转前后的两个图形全等 | D. | 图形上每一点所经过的路程相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
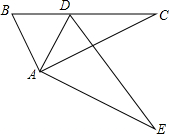 如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.
如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
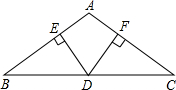 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com