
【题目】如图,在平面直角坐标系中,⊙P的圆心坐标是(5,a)(a>5),半径为5,函数y=x的图象被⊙P截得的弦AB的长为8,则a的值是( )
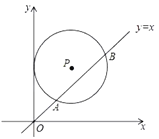
A. 8 B. 5+3![]() C. 5
C. 5![]() D. 5+
D. 5+![]()
科目:初中数学 来源: 题型:
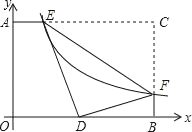
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=![]() (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
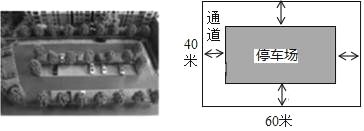
【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安某学校为了改善办学条件,计划购置一批电子白板和台式电脑.经招投标,购买一台电子白板比购买2台台式电脑多3000元,购买2台电子白板和3台台式电脑共需2.7万元.
(1)设购买一台台式电脑需![]() 元,购买一台电子白板需 元(用含
元,购买一台电子白板需 元(用含![]() 的代数式表示)
的代数式表示)
(2)求购买一台电子白板和一台台式电脑各需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com