
【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.
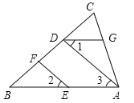
请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】国学经典进校园,传统文化润心灵,某校开设了“围棋入门”、“诗歌汉字”、“翰墨飘香”、“史学经典”四门拓展课(每位学生必须且只选其中一门).
(1)学校对八年级部分学生进行选课调查,
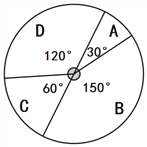

得到如图所示的统计图,请估计该校八年级420名学生选“诗歌汉字”的人数.
(2)“翰墨飘香”书画社的甲、乙、丙三人的书法水平相当,学校决定从这三名同学中任选两名参加市书法比赛,求甲和乙被选中的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点A6的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
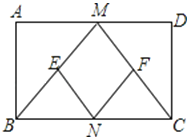
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABO中,∠AOB=90°,OA=![]() ,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
(1)如图①,当E点恰好落在线段AB上时,求E点坐标;
(2)在(Ⅰ)问的条件下,将△ODE沿x轴的正半轴向右平移得到△O′D′E′,O′E′、D′E′分别交AB于点G、F(如图②)求证OO′=E′F;
(3)若点D沿x轴正半轴向右移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式.
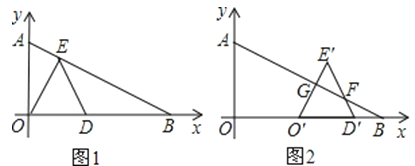
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() (a≠0)的图象与反比例函数
(a≠0)的图象与反比例函数![]() 的图象交于第二、第四象限内的A、B两点,与
的图象交于第二、第四象限内的A、B两点,与![]() 轴交于点C,过点A作AH⊥
轴交于点C,过点A作AH⊥![]() 轴,垂足为点H,OH=3,tan∠AOH=
轴,垂足为点H,OH=3,tan∠AOH=![]() ,点B的坐标为(
,点B的坐标为(![]() ,-2).
,-2).
(1)求该反比例函数和一次函数的解析式;
(2)求△AHO的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,BC=AC,CE是过点C的一条直线,且A、B在CE的异侧,AD⊥CE于D,BE⊥CE于E.
(1)求证:AD=DE+BE.
(2)若直线CE绕点C旋转,使A、B在CE的同侧时(如图②),AD与DE、BE的关系如何?请予以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com