
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
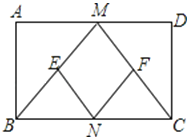
【答案】(1)证明见解析;(2)四边形MENF是菱形;理由见解析.
【解析】(1)由矩形的性质得出AB=DC,∠A=∠D,再由M是AD的中点,根据SAS即可证明△ABM≌△DCM;
(2)先由(1)得出BM=CM,再由已知条件证出ME=MF,EN、FN是△BCM的中位线,即可证出EN=FN=ME=MF,得出四边形MENF是菱形.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵M是AD的中点,
∴AM=DM,
在△ABM和△DCM中,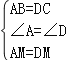 ,
,
∴△ABM≌△DCM(SAS);
(2)解:四边形MENF是菱形;理由如下:
由(1)得:△ABM≌△DCM,
∴BM=CM,
∵E、F分别是线段BM、CM的中点,
∴ME=BE=![]() BM,MF=CF=
BM,MF=CF=![]() CM,
CM,
∴ME=MF,
又∵N是BC的中点,
∴EN、FN是△BCM的中位线,
∴EN=![]() CM,FN=
CM,FN=![]() BM,
BM,
∴EN=FN=ME=MF,
∴四边形MENF是菱形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.
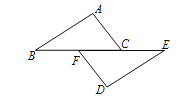
(1)选择的条件是 (填序号)
(2)证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
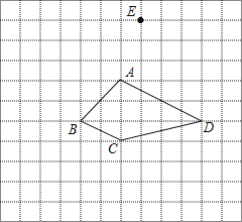
【题目】如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点.
(1)作出四边形ABCD关于直线AC对称的四边形AB′CD′;
(2)求四边形ABCD的面积;
(3)若在直线AC上有一点P,使得P到D、E的距离之和最小,请作出点P(请保留作图痕迹),且求出PC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.
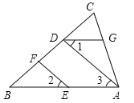
请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
查看答案和解析>>
科目:初中数学 来源: 题型:
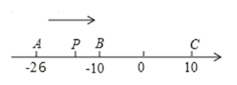
【题目】已知数轴上有 A、B、C 三点,分别表示有理数-26,-10,10,动点 P 从 A 出发,以每秒 1 个 单位的速度向终点 C 移动,设点 P 移动时间为 t 秒.
(1)用含 t 的代数式表示 P 到点 A 和点C 的距离:PA= ,PC=
(2)当点 P 运动到 B 点时,点 Q 从 A 点出发,以每秒 3 个单位的速 度向 C 点运动,Q 点到达 C 点后,再立即以同样的速度返回,当点 P 运动到点 C 时,P、Q 两点运动停止,
①当 P、Q 两点运动停止时,求点 P 和点 Q 的距离;
②求当 t 为何值时 P、Q 两点恰好在途中相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com