
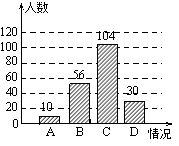
����Ŀ������̼����������ͬ�����������������������Ĺ������г���������д�����ʵ����������̨������ij����ͷ���ѡȡ��������е����������������������Ŷ��ʹ��һ�ι������г������������ε�������Ϊ���������A��ÿ�춼����B������ʹ����C��ż��ʹ����D����δʹ��������ε������������������������ͳ��ͼ��

����ͼ�е���Ϣ������������⣺
��1�������� �����������
��2����ȫ����ͳ��ͼ��
��3������ͳ�ƽ������������46�������������ÿ�춼���������г�������Լ�ж����ˣ�
���𰸡���1��200��
��2��ͼ�μ�������
��3������ÿ�춼�ù������г�������ԼΪ2��3������
��������
�����������1���ɴ�δʹ�õ���30����ռ15%����30ȥ����15%���ɵ���
��������ͼ�ɵ�A��B��C����������200ȥ���ٷֱ�������A�İٷֱ�=1-28%-52%-15%=5%����Ȼ��ȫ����ͼ������
��46�����A��ռ�İٷֱ�����5%���ɵ���
�����������1��200��
��2����ͼ��
��3��46��5%��2��3�����������𣺹���ÿ�춼�ù������г�������ԼΪ2��3������


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ3��������OABC�����������������ϣ�������y����x2��bx��c������A��C����x�ύ����һ��D��PΪ��һ��������������һ�㣬��P����y���ƽ���߽�x ���ڵ�Q����AC�ڵ�E.
(1)�������߽���ʽ����D��������
(2)��E����x���ƽ���߽�AB�ڵ�F������P��E��FΪ���������������ODC���ƣ����P������
(3)��P����PH��AC��H���Ƿ���ڵ�Pʹ��PEH���ܳ�ȡ�����ֵ�������ڣ��������P���꼰��PEH�ܳ������ֵ���������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
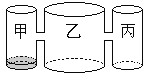
����Ŀ��ʵ�����ˮƽ�������мס��ҡ�������Բ���������������㹻�ߣ�������뾶֮��Ϊ1��2��1������������ͬ�Ĺ�����������5cm�߶ȴ���ͨ�������ӵ���������5cm���������������У�ֻ�м�����ˮ��ˮλ��1cm����ͼ��ʾ����ÿ����ͬʱ���Һͱ�ע����ͬ����ˮ����ʼעˮ1���ӣ��ҵ�ˮλ����![]() cm����ʼע�� ���ӵ�ˮ�������ҵ�ˮλ�߶�֮����0��5cm��
cm����ʼע�� ���ӵ�ˮ�������ҵ�ˮλ�߶�֮����0��5cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ����
��5����2.626626662����0����������![]() ��0.12��������6����
��0.12��������6����
��1���������ϣ�{____________________��}��
��2�����������ϣ�{___________________ ��}��
��3�����������ϣ�{__________________��}��
��4���������ϣ�{___________________ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��ax��b(a��0)��ͼ���뷴��������y��![]() (k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��
(k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��![]() ����B������Ϊ(m����2)��
����B������Ϊ(m����2)��
(1)���AHO���ܳ���
(2)��÷�����������һ�κ����Ľ���ʽ��

���𰸡�(1)��AHO���ܳ�Ϊ12��(2) �����������Ľ���ʽΪy��![]() ��һ�κ����Ľ���ʽΪy����
��һ�κ����Ľ���ʽΪy����![]() x��1.
x��1.
���������������: ��1���������к������ɵ�AH�ij������ݹ��ɶ������ɵ�AO�ij������������ε��ܳ����ɵô𰸣�
��2�����ݴ���ϵ�������ɵú�������ʽ��
�����������1����OH=3��tan��AOH=![]() ����
����
AH=4����A��-4��3����
�ɹ��ɶ�������
AO=![]() =5��
=5��
��AHO���ܳ�=AO+AH+OH=3+4+5=12��
��2����A���������y=![]() ��k��0������
��k��0������
k=-4��3=-12��
�����������Ľ���ʽΪy=![]() ��
��
��y=-2ʱ��-2=![]() �����x=6����B��6��-2����
�����x=6����B��6��-2����
��A��B���������y=ax+b����
![]() ��
��
��� ��
��
һ�κ����Ľ���ʽΪy=-![]() x+1��
x+1��
���㣺������������һ�κ����Ľ������⣮
�����͡������
��������
25
����Ŀ����ͼ����֪��A��C�ֱ��ڡ�GBE�ı�BG��BE�ϣ���AB=AC��AD��BE����GBE��ƽ������AD���ڵ�D������CD��
��֤����AB=AD��
��CDƽ�֡�ACE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y����x+4�ֱ���x�ᡢy�ύ�ڵ�A��B��˫����![]() ��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ���ڸ�������OA������OB����MON���������¶��壺��������OA��OB��ɵġ�AOB��ƽ����OT���ڡ�MON���ڲ����OM��ON�ϣ��������OA������OB���ڡ�MON�ں��Գ�.���磬ͼ1������OA������OB���ڡ�MON�ں��Գ�

��֪����ͼ2����ƽ���ڣ���AOM=10������MON=20��
��1��������������![]() ��
��![]() ��λ����ͼ3��ʾ����
��λ����ͼ3��ʾ����![]() ��
��![]() �����������������У�������OA���ڡ�MON�ں��ԳƵ�������_____________
�����������������У�������OA���ڡ�MON�ں��ԳƵ�������_____________
��2������OC��ƽ�����Ƶ�O��ת��һ�������ߣ�������OA������OC���ڡ�MON�ں��Գƣ����COM=x������x��ȡֵ��Χ��
��3����ͼ4����AOE=��EOH=2��FOH=20�����ֽ�����OH�Ƶ�O��ÿ��1�����ٶ�˳ʱ����ת��ͬʱ������OE��OF�Ƶ�O����ÿ��3�����ٶ�˳ʱ����ת.����ת��ʱ��Ϊt�룬��![]() .����FOE���ڲ����������ٴ���һ����OΪ���������������OH���ڡ�MON�ں��Գƣ�ֱ��д��t��ȡֵ��Χ.
.����FOE���ڲ����������ٴ���һ����OΪ���������������OH���ڡ�MON�ں��Գƣ�ֱ��д��t��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ƻ���������̨���ԣ��ִ������̳��˽ͬһ���ͺŵĵ��Ա��۾�Ϊ6000Ԫ�����Ҷ�����һ�����Ż�.���̳����Ż��������±���ʾ��
�̳� | �Ż����� |
���̳� | ��һ̨��ԭ���շѣ������ÿ̨�Ż�25% |
���̳� | ÿ̨�Ż�20% |
(1)��ѧУ����![]() ̨���ԣ�ѡ����̳�ʱ���������Ϊ
̨���ԣ�ѡ����̳�ʱ���������Ϊ![]() Ԫ��ѡ�����̳�ʱ���������Ϊ
Ԫ��ѡ�����̳�ʱ���������Ϊ![]() Ԫ����ֱ����
Ԫ����ֱ����![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵʽ.
֮��Ĺ�ϵʽ.
(2)ʲô����£������̳����շ���ͬ��ʲô����£������̳�������Żݣ�ʲô����£������̳�������Żݣ�
(3)������Ϊ���裬�ƻ��Ӽ������̳�һ������10̨���ԣ���֪���̳����˷�Ϊÿ̨50Ԫ�����̳����˷�Ϊÿ̨60Ԫ�������˷�Ϊ![]() Ԫ���Ӽ��̳�����
Ԫ���Ӽ��̳�����![]() ̨���ԣ��ڼ��̳��Ŀ��ֻ��4̨������£������������˷����٣������˷��Ƕ��٣�
̨���ԣ��ڼ��̳��Ŀ��ֻ��4̨������£������������˷����٣������˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com