
”¾ĢāÄæ”æČēĶ¼¢ŁÅ×ĪļĻßy£½ax2+bx+4£Øa”Ł0£©ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćA£Ø©1£¬0£©£¬B£Ø4£¬0£©£¬µćCČżµć£®
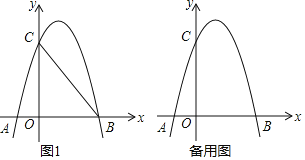
£Ø1£©ŹŌĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćD£Ø3£¬m£©ŌŚµŚŅ»ĻóĻŽµÄÅ×ĪļĻßÉĻ£¬Į¬½ÓBC£¬BD£®ŹŌĪŹ£¬ŌŚ¶Ō³ĘÖį×ó²ąµÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µćP£¬Āś×ć”ĻPBC£½”ĻDBC£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćPµćµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©µćNŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬µćMŌŚÅ×ĪļĻßÉĻ£¬µ±ŅŌM”¢N”¢B”¢CĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³öµćMµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©y£½©x2+3x+4£»£Ø2£©“ęŌŚ£®P£Ø©![]() £¬
£¬![]() £©£®£Ø3£©
£©£®£Ø3£©![]()
![]()
![]()
”¾½āĪö”æ
£Ø1£©½«A,B,CČżµć“śČėy£½ax2+bx+4Ēó³öa,b,cÖµ£¬¼“æÉČ·¶Ø±ķ“ļŹ½£»
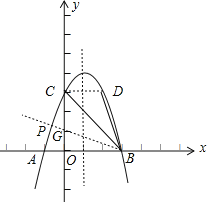
£Ø2£©ŌŚyÖįÉĻČ”µćG£¬Ź¹CG£½CD£½3£¬¹¹½Ø”÷DCB”Õ”÷GCB£¬ĒóÖ±ĻßBGµÄ½āĪöŹ½£¬ŌŁĒóÖ±ĻßBGÓėÅ×ĪļĻß½»µć×ų±ź¼“ĪŖPµć£¬
£Ø3£©øł¾ŻĘ½ŠŠĖıߊĪµÄ¶Ō±ßĘ½ŠŠĒŅĻąµČ£¬ĄūÓĆĘ½ŅʵĊŌÖŹĮŠ³ö·½³ĢĒó½ā£¬·ÖĒéæöĢÖĀŪ.
½ā£ŗČēĶ¼£ŗ
£Ø1£©”ßÅ×ĪļĻßy£½ax2+bx+4£Øa”Ł0£©ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćA£Ø©1£¬0£©£¬B£Ø4£¬0£©£¬µćCČżµć£®
”ą ![]() ½āµĆ
½āµĆ![]()
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½©x2+3x+4£®
£Ø2£©“ęŌŚ£®ĄķÓÉČēĻĀ£ŗ
y£½©x2+3x+4£½©£Øx©![]() £©2+
£©2+![]() £®
£®
”ßµćD£Ø3£¬m£©ŌŚµŚŅ»ĻóĻŽµÄÅ×ĪļĻßÉĻ£¬
”ąm£½4£¬”ąD£Ø3£¬4£©£¬”ßC£Ø0£¬4£©
”ßOC£½OB£¬”ą”ĻOBC£½”ĻOCB£½45”ć£®
Į¬½ÓCD£¬”ąCD”ĪxÖį£¬
”ą”ĻDCB£½”ĻOBC£½45”ć£¬
”ą”ĻDCB£½”ĻOCB£¬
ŌŚyÖįÉĻČ”µćG£¬Ź¹CG£½CD£½3£¬
ŌŁŃÓ³¤BG½»Å×ĪļĻßÓŚµćP£¬ŌŚ”÷DCBŗĶ”÷GCBÖŠ£¬CB£½CB£¬”ĻDCB£½”ĻOCB£¬CG£½CD£¬
”ą”÷DCB”Õ”÷GCB£ØSAS£©
”ą”ĻDBC£½”ĻGBC£®
ÉčÖ±ĻßBP½āĪöŹ½ĪŖyBP£½kx+b£Øk”Ł0£©£¬°ŃG£Ø0£¬1£©£¬B£Ø4£¬0£©“śČė£¬µĆ
k£½©![]() £¬b£½1£¬
£¬b£½1£¬
”ąBP½āĪöŹ½ĪŖyBP£½©![]() x+1£®
x+1£®
yBP£½©![]() x+1£¬y£½©x2+3x+4
x+1£¬y£½©x2+3x+4
µ±y£½yBP Ź±£¬©![]() x+1£½©x2+3x+4£¬
x+1£½©x2+3x+4£¬
½āµĆx1£½©![]() £¬x2£½4£ØÉįČ„£©£¬
£¬x2£½4£ØÉįČ„£©£¬
”ąy£½![]() £¬”ąP£Ø©
£¬”ąP£Ø©![]() £¬
£¬![]() £©£®
£©£®
£Ø3£©![]()
![]()
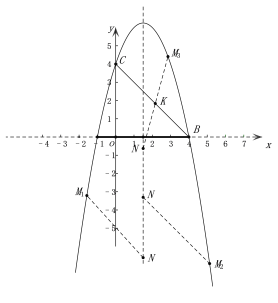
![]() ĄķÓÉČēĻĀ£¬ČēĶ¼
ĄķÓÉČēĻĀ£¬ČēĶ¼
B(4£¬0),C(0£¬4) £¬Å×ĪļĻ߶Ō³ĘÖįĪŖÖ±Ļß![]() £¬
£¬
ÉčN(![]() £¬n)£¬M(m, ©m2+3m+4)
£¬n)£¬M(m, ©m2+3m+4)
µŚŅ»ÖÖĒéæö£ŗµ±MNÓėBCĪŖ¶Ō±ß¹ŲĻµŹ±£¬MN”ĪBC,MN=BC,
”ą4-![]() =0-m£¬”ąm=
=0-m£¬”ąm=![]()
”ą©m2+3m+4=![]() ,
,
”ą![]() £»
£»
»ņ”ą0-![]() =4-m£¬
=4-m£¬
”ąm=![]()
”ą©m2+3m+4=![]() ,
,
”ą![]() £»
£»
µŚ¶žÖÖĒéæö£ŗµ±MNÓėBCĪŖ¶Ō½ĒĻß¹ŲĻµ£¬MNÓėBC½»µćĪŖK,ŌņK(2,2)£¬
”ą
”ąm=![]()
”ą©m2+3m+4=![]()
”ą![]()
×ŪÉĻĖłŹö£¬µ±ŅŌM”¢N”¢B”¢CĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬µćMµÄ×ų±źĪŖ![]()
![]()
![]() .
.


 ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø
ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø ½šÅĘ½ĢøØÅąÓÅÓÅŃ”¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
½šÅĘ½ĢøØÅąÓÅÓÅŃ”¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°±¼ÅÜ°É£¬ŠÖµÜ£””±½ŚÄæ×飬Ō¤Éč¼ĘŅ»øöŠĀµÄÓĪĻ·£ŗ”°±¼ÅÜ”±Ā·Ļߊč¾A”¢B”¢C”¢DĖĵŲ£®ČēĶ¼£¬ĘäÖŠA”¢B”¢CČżµŲŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬DµŲŌŚAµŲ±±Ę«¶«30”ć·½Ļņ”¢ŌŚCµŲ±±Ę«Ī÷45”ć·½Ļņ£®CµŲŌŚAµŲ±±Ę«¶«75”ć·½Ļņ£®ĒŅBD=BC=30m£®“ÓAµŲµ½DµŲµÄ¾ąĄėŹĒ£Ø””””£©

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ±¾×Å”°Äžæɱø¶ų²»ÓĆ£¬²»æÉÓƶųĪŽ±ø”±µÄĄķÄī£¬1ŌĀ26ČÕÖ£ÖŻŹŠĪÆŹŠÕžø®¾ö¶Ø½öÓĆ10ĢģŹ±¼ä½ØÉč³ÉÖ£ÖŻ°ę”°Š”ĢĄÉ½Ņ½Ōŗ”±£¬Ņ»“óÅś”°ĶØŠŠÕß”±“ÓĖÄĆę°Ė·½½ō¼Æ³ŪŌ®£¬170ÓąĢØ»śŠµÖēŅ¹²»Ķ£µŲƦĀµŌŚæ¹ŅßŅ»Ļߣ¬ČēĶ¼1ĖłŹ¾ŹĒ½ØÖžŹ¦øµÕżŌŚ¶Ō³¤·½ĢåŠĶ¼Æ×°Ļä·æ½ųŠŠĘšµõČĪĪń£¬ČēĶ¼2ĖłŹ¾£¬½ØÖžŹ¦øµĶعż²Ł×Ż»śŠµ±Ū£ØĶ¼ÖŠµÄOA£©Ą“Ķź³ÉĘšµõ£¬ŌŚĘšµõ¹ż³ĢÖŠŹ¼ÖÕ±£³Ö¼Æ×°ĻäÓėµŲĘ½ĆęĘ½ŠŠ£¬ĘšµõĒ°¹¤ČĖŹ¦øµ²āµĆ”ĻPDE£½45”ć£¬”ĻPED£½60”ć£¬OA³¤20Ć×£¬DE³¤6Ć×£¬EH³¤3Ć×£¬Oµ½µŲĆęµÄ¾ąĄėOQ³¤2Ć×£¬AP³¤4Ć×£¬AP”ĪOQ£¬µ±µõ±ŪOAŗĶĖ®Ę½·½ĻņµÄ¼Š½ĒĪŖ53¶ČŹ±£¬Ēó¼Æ×°Ļäµ×²æ¾ąĄėµŲĆęµÄøß¶Č£®£Ø×¢£ŗ“ÓĘšµõĒ°µ½Ęšµõ½įŹųŹ¼ÖÕ±£³Ö”ĻPDE£¬”ĻPEDµÄ¶ČŹż²»±ä£©
£Ø½į¹ū¾«Č·µ½1m£¬²Īæ¼Źż¾Ż![]() ”Ö1.41£¬
”Ö1.41£¬![]() ”Ö1.73£¬tan53”ć”Ö
”Ö1.73£¬tan53”ć”Ö![]() £¬sin53”ć”Ö
£¬sin53”ć”Ö![]() £¬cos53”ć”Ö
£¬cos53”ć”Ö![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻABC=80”ć£¬”ĻBAC=40”ć.
£Ø1£©³ß¹ę×÷Ķ¼×÷³öABµÄ“¹Ö±Ę½·ÖĻßDE£¬·Ö±šÓėAC”¢AB½»ÓŚµćD”¢E£®²¢Į¬½įBD£»£Ø±£Įō×÷Ķ¼ŗŪ¼££¬²»Š“×÷·Ø£©

£Ø2£©Ö¤Ć÷£ŗ”÷ABC”×”÷BDC£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ÓŠŅ»ÕžŲŠĪÖ½Ę¬![]() ŅŃÖŖ
ŅŃÖŖ![]() ĻÖ½«Ö½Ę¬½ųŠŠČēĻĀ²Ł×÷:ĻÖ½«Ö½Ę¬ŃŲÕŪŗŪ
ĻÖ½«Ö½Ę¬½ųŠŠČēĻĀ²Ł×÷:ĻÖ½«Ö½Ę¬ŃŲÕŪŗŪ![]() ½ųŠŠÕŪµž£¬Ź¹µć
½ųŠŠÕŪµž£¬Ź¹µć![]() ĀäŌŚ
ĀäŌŚ![]() ±ßÉĻµÄµć
±ßÉĻµÄµć![]() “¦£¬µć
“¦£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ(ČēĶ¼2)£»Č»ŗó½«Ö½Ę¬ŃŲÕŪŗŪ
ÉĻ(ČēĶ¼2)£»Č»ŗó½«Ö½Ę¬ŃŲÕŪŗŪ![]() ½ųŠŠµŚ¶ž“ĪÕŪµž£¬Ź¹µć
½ųŠŠµŚ¶ž“ĪÕŪµž£¬Ź¹µć![]() ĀäŌŚµŚŅ»“ĪµÄÕŪŗŪ
ĀäŌŚµŚŅ»“ĪµÄÕŪŗŪ![]() ÉĻµÄµć
ÉĻµÄµć![]() “¦£¬µć
“¦£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ(ČēĶ¼3)£¬øų³öĖÄøö½įĀŪ£ŗ¢Ł
ÉĻ(ČēĶ¼3)£¬øų³öĖÄøö½įĀŪ£ŗ¢Ł![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() £»¢Ś
£»¢Ś![]() µÄÖܳ¤ĪŖ
µÄÖܳ¤ĪŖ![]() ¢Ū
¢Ū![]() £»¢Ü
£»¢Ü![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø £©
ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø £©
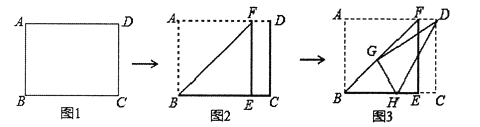
A.¢Ł¢Ś¢ŪB.¢Ł¢Ś¢ÜC.¢Ł¢Ū¢ÜD.¢Ś¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³Ń§Š£ĪŖĮĖ½ā¾ÅÄź¼¶µÄ600ĆūѧɜĆæĢģµÄ×ŌÖ÷ѧĻ°Ēéæö£¬Ė껜³é²éĮĖ¾ÅÄź¼¶µÄ²æ·Öѧɜ£¬²¢µ÷²éĖūĆĒĆæĢģ×ŌÖ÷ѧĻ°µÄŹ±¼ä£®øł¾Żµ÷²é½į¹ū£¬ÖĘ×÷ĮĖĮ½ø±²»ĶźÕūµÄĶ³¼ĘĶ¼£ØĶ¼1Ķ¼2£©£¬Ēėøł¾ŻĶ³¼ĘĶ¼ÖŠµÄŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
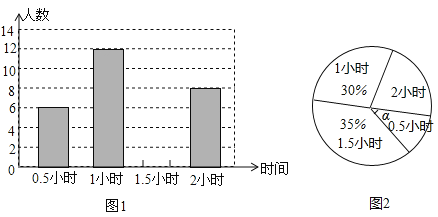
£Ø1£©±¾“Īµ÷²éµÄѧɜČĖŹżŹĒ ČĖ£»
£Ø2£©Ķ¼2ÖŠ½Ē![]() ŹĒ ¶Č£»
ŹĒ ¶Č£»
£Ø3£©½«Ķ¼1ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø4£©¹ĄĖćøĆŠ£¾ÅÄź¼¶Ń§Éś×ŌÖ÷ѧĻ°²»ÉŁÓŚ1.5Š”Ź±ÓŠ¶ąÉŁČĖ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«ŗÆŹży=![]() £Øx©2£©2+1µÄĶ¼ĻóŃŲyÖįĻņÉĻĘ½ŅʵƵ½Ņ»ĢõŠĀŗÆŹżµÄĶ¼Ļó£¬ĘäÖŠµćA£Ø1£¬m£©£¬B£Ø4£¬n£©Ę½ŅĘŗóµÄ¶ŌÓ¦µć·Ö±šĪŖµćA'”¢B'£®ČōĒśĻ߶ĪABÉعżµÄĆ껿ĪŖ9£ØĶ¼ÖŠµÄŅõÓ°²æ·Ö£©£¬ŌņŠĀĶ¼ĻóµÄŗÆŹż±ķ“ļŹ½ŹĒ£Ø””””£©
£Øx©2£©2+1µÄĶ¼ĻóŃŲyÖįĻņÉĻĘ½ŅʵƵ½Ņ»ĢõŠĀŗÆŹżµÄĶ¼Ļó£¬ĘäÖŠµćA£Ø1£¬m£©£¬B£Ø4£¬n£©Ę½ŅĘŗóµÄ¶ŌÓ¦µć·Ö±šĪŖµćA'”¢B'£®ČōĒśĻ߶ĪABÉعżµÄĆ껿ĪŖ9£ØĶ¼ÖŠµÄŅõÓ°²æ·Ö£©£¬ŌņŠĀĶ¼ĻóµÄŗÆŹż±ķ“ļŹ½ŹĒ£Ø””””£©

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬AB=5cm£¬BD=8cm£®µćP“ÓµćB³ö·¢£¬ŃŲBA·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖ![]() £»Ķ¬Ź±£¬µćQ“ÓµćD³ö·¢£¬ŃŲDA·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖ1cm/s£®¹żµćP×÷PN”ĪBC·Ö±š½»BD£¬CDÓŚµćM,N£¬Į¬½ÓQM£¬QN£®ÉčŌĖ¶ÆŹ±¼äĪŖ
£»Ķ¬Ź±£¬µćQ“ÓµćD³ö·¢£¬ŃŲDA·½ĻņŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖ1cm/s£®¹żµćP×÷PN”ĪBC·Ö±š½»BD£¬CDÓŚµćM,N£¬Į¬½ÓQM£¬QN£®ÉčŌĖ¶ÆŹ±¼äĪŖ![]() £®½ā“šĻĀĮŠĪŹĢā£ŗ
£®½ā“šĻĀĮŠĪŹĢā£ŗ
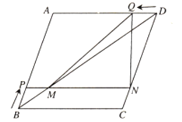
£Ø1£©µ±![]() ĪŖŗĪÖµŹ±£¬µć
ĪŖŗĪÖµŹ±£¬µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() µÄ“¹Ö±Ę½·ÖĻßÉĻ£æ
µÄ“¹Ö±Ę½·ÖĻßÉĻ£æ
£Ø2£©Éč![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½£»
µÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ![]() £¬Ź¹
£¬Ź¹![]() µÄĆ껿ĪŖĮāŠĪ
µÄĆ껿ĪŖĮāŠĪ![]() Ć껿µÄ
Ć껿µÄ![]() £¬Čō“ęŌŚ£¬Ēó³ö
£¬Čō“ęŌŚ£¬Ēó³ö![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø4£©ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ![]() £¬Ź¹
£¬Ź¹![]() ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³ö
ĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³ö![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬CĪŖ”ŃOÉĻŅ»µć£¬”ĻABCµÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬DE”ĶBCÓŚµćE£®
£Ø1£©ŹŌÅŠ¶ĻDEÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©¹żµćD×÷DF”ĶABÓŚµćF£¬ČōBE=3![]() £¬DF=3£¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®
£¬DF=3£¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com