
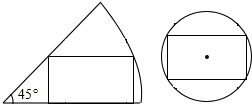
 一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )
一张圆心角为45°的扇形纸板和一张圆形纸板分别剪成两个大小相同的长方形,若长方形长和宽的比值为2:1,则扇形纸板和圆形纸板的半径之比为( )| A. | 2$\sqrt{2}$:1 | B. | $\sqrt{5}$:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
分析 先画出图形,设长方形的宽为x,则长为2x,根据勾股定理,分别求出扇形和圆的半径(用x表示),最后求出比值即可.
解答 解: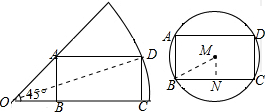 连接OD,BM,作MN⊥BC,
连接OD,BM,作MN⊥BC,
设长方形的宽为x,则长为2x,
∵∠AOB=45°,四边形ABCD为矩形,
∴∠OAB=45°,
∴OB=AB=x,
则OC=3x,
∴OD=$\sqrt{{x}^{2}{+(3x)}^{2}}$=$\sqrt{10}$x,
∵AB=x,
∴BN=x,MN=$\frac{1}{2}$x,
∴BM=$\sqrt{{(\frac{1}{2}x)}^{2}{+x}^{2}}$=$\frac{\sqrt{5}}{2}x$,
∴$\frac{OD}{BM}$=$2\sqrt{2}$:1,
故选A.
点评 本题主要考查了勾股定理,垂径定理,矩形的性质,设长方形的宽为x,则长为2x,利用勾股定理定理是解答此题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:选择题
| 居民(户) | 1 | 2 | 8 | 6 | 2 | 1 |
| 月用水量(吨) | 4 | 5 | 8 | 12 | 15 | 20 |
| A. | 平均数是10(吨) | B. | 众数是8(吨) | C. | 中位数是10(吨) | D. | 样本容量是20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形纸片ABCD的对称中心为O,翻折∠A使顶点A重合于对角线AC上一点P,EF是折痕:
正方形纸片ABCD的对称中心为O,翻折∠A使顶点A重合于对角线AC上一点P,EF是折痕:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
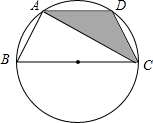 如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.
如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com