
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 . 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第![]() s或
s或![]() s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD 
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D有下列五个条件①AE=DE ②BE=CE ③AB=DC ④∠ABC=∠DCB⑤AC=BD能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明。
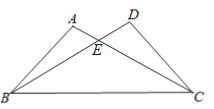
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,② ![]() ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组![]() 的关联方程是________
的关联方程是________
(2)若不等式组  的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
(3)若方程 3-x=2x,3+x= ![]() 都是关于 x 的不等式组
都是关于 x 的不等式组 ![]() 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com