【题目】解方程： 
．
【答案】解：方程两边乘（x﹣2）（x+2），
得x（x+2）﹣8=x﹣2，
x2+x﹣6=0，
（x+3）（x﹣2）=0，
解得x1=﹣3，x2=2．
经检验：x1=﹣3是原方程的根，x2=2是增根．
∴原方程的根是x=﹣3
【解析】观察可得最简公分母是（x﹣2）（x+2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．
【考点精析】本题主要考查了因式分解法和去分母法的相关知识点，需要掌握已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势；先约后乘公分母，整式方程转化出．特殊情况可换元，去掉分母是出路．求得解后要验根，原留增舍别含糊才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，对角线AC与BD交于点O，若增加一个条件，使ABCD成为菱形，下列给出的条件不正确的是（ ） 
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ） 
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为5cm，则圆心O到弦CD的距离为（ ） 
A.
cm
B.3cm
C.3 
cm
D.6cm
查看答案和解析>>
科目：初中数学 来源： 题型：
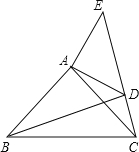
【题目】已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．
（1）求证：△BAD≌△CAE；
（2）试猜想BD、CE有何特殊位置关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2+bx+c的图象与y轴交于点C（0，﹣6），与x轴的一个交点坐标是A（﹣2，0）． 
（1）求二次函数的解析式，并写出顶点D的坐标；
（2）将二次函数的图象沿x轴向左平移 
个单位长度，当 y＜0时，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道：“两边及其中一边的对角分别相等的两个三角形不一定全等”．但是，小亮发现：当这两个三角形都是锐角三角形时，它们会全等，除小亮的发现之外，当这两个三角形都是时，它们也会全等；当这两个三角形其中一个三角形是锐角三角形，另一个是时，它们一定不全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．
（1）问线段EC与BF数量关系和位置关系？并给予证明．
（2）连AM，请问∠AME的大小是多少，如能求写出过程；不能求，写出理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
