
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
(1)问线段EC与BF数量关系和位置关系?并给予证明.
(2)连AM,请问∠AME的大小是多少,如能求写出过程;不能求,写出理由.

【答案】(1)EC⊥BF, EC=BF(2)∠AME=45°.
【解析】
(1)先由条件可以得出∠EAC=∠FAB,再证明△EAC≌△BAF就可以得出结论.
(2)作AN⊥EC,AH⊥BF,通过(1)中已知条件证明Rt△AMH ≌Rt△AMN,即可求解.
(1)理由: 设AB与EC的交点为G
∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠FAB
在△EAC和△BAF中,AE=AB, ∠EAC=∠FAB,AF=AC
∴△EAC≌△BAF
∴EC=BF, ∠AEC=∠FBA
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°
∴∠BME=90°,
∴EC⊥BF.
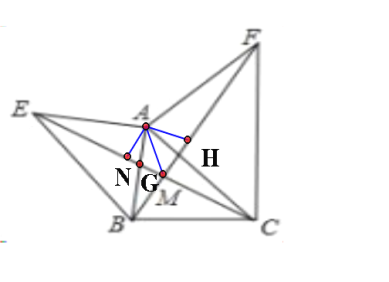
(2)作AN⊥EC,AH⊥BF
∵△EAC≌△BAF,AN⊥EC,AH⊥BF
∴AH=AN
∵AM⊥EC,AN⊥BF
∴Rt△AMH 和Rt△AMN中,AH=AN,AM=AM
∴Rt△AMH ≌Rt△AMN(HL)
∴∠AMH =∠AMN
∵EC⊥BF
∴∠AME=45°.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.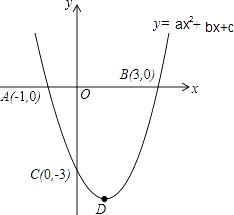
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
例:已知: ![]() ,
,
求: ![]() 和
和 ![]() 的值.
的值.
解:![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
解决问题:
(1)若 ![]() ,求 x、y 的值;
,求 x、y 的值;
(2)已知 ![]() ,
,![]() ,
,![]() 是
是 ![]() 的三边长且满足
的三边长且满足 ![]() ,
,
①直接写出a=__________.b=___________.
②若![]() 是
是 ![]() 中最短边的边长(即c<a;c<b),且
中最短边的边长(即c<a;c<b),且 ![]() 为整数,直接写出
为整数,直接写出 ![]() 的值可能是 .
的值可能是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
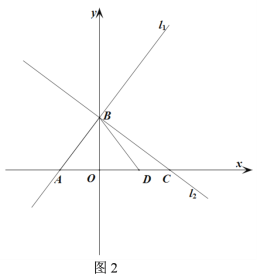
【题目】如图,直线![]() :
:![]() 与x轴、y轴分别交于A、B两点,直线
与x轴、y轴分别交于A、B两点,直线![]() 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、![]() 两点,且
两点,且![]() ︰
︰![]() ︰
︰![]() .
.
(1)求直线![]() 的解析式,并判断
的解析式,并判断![]() 的形状;
的形状;
(2)如图![]() ,
,![]() 为直线
为直线![]() 上一点,横坐标为
上一点,横坐标为![]() ,
,![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 最小时,将线段
最小时,将线段![]() 沿射线
沿射线![]() 方向平移,平移后
方向平移,平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 最小时,求点
最小时,求点![]() 的坐标;
的坐标;
(3)如图![]() ,将
,将![]() 沿着
沿着![]() 轴翻折,得到
轴翻折,得到![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() )得到
)得到![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .当
.当![]() 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com