
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
【答案】①②③
【解析】解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1﹣x,
∵△CEF为等腰直角三角形,
∴EF= ![]() CE,即2x=
CE,即2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,
﹣1,
∴EF=2( ![]() ﹣1),
﹣1),
∴CH= ![]() EF=
EF= ![]() ﹣1,所以②正确.
﹣1,所以②正确.
故答案为①②③.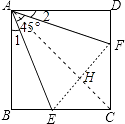
先证明Rt△ABE≌Rt△ADF得到∠1=∠2,易得∠1=∠2=∠22.5°,于是可对①进行判断;连结EF、AC,它们相交于点H,如图,利用Rt△ABE≌Rt△ADF得到BE=DF,则CE=CF,接着判断AC垂直平分EF,AH平分∠EAF,于是利用角平分线的性质定理得到EB=EH,FD=FH,则可对③④进行判断;设BE=x,则EF=2x,CE=1﹣x,利用等腰直角三角形的性质得到2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,则可对④进行判断.本题考查了四边形的综合题:熟练掌握正方形的性质和角平分线的性质定理.解决本题的关键是证明AC垂直平分EF.
﹣1,则可对④进行判断.本题考查了四边形的综合题:熟练掌握正方形的性质和角平分线的性质定理.解决本题的关键是证明AC垂直平分EF.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0). 
(1)求二次函数的解析式,并写出顶点D的坐标;
(2)将二次函数的图象沿x轴向左平移 ![]() 个单位长度,当 y<0时,求x的取值范围.
个单位长度,当 y<0时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
(1)问线段EC与BF数量关系和位置关系?并给予证明.
(2)连AM,请问∠AME的大小是多少,如能求写出过程;不能求,写出理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学校图书馆上个月借阅情况,管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计,并绘制了下列不完整的统计图,请根据图中信息解答下列问题: 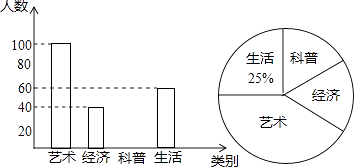
(1)上个月借阅图书的学生有多少人?扇形统计图中“艺术”部分的圆心角度数是多少?
(2)把条形统计图补充完整;
(3)从借阅情况分析,如果要添置这四类图书300册,请你估算“科普”类图书应添置多少册合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张背面完全相同的数字牌,它们的正面分别印有数字“1”、“2”、“3”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字a、b、c,则以a、b、c为边长正好构成等边三角形的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点, ![]() ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F. 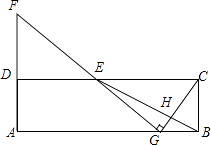
(1)求证: ![]() ;
;
(2)若∠CGF=90°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
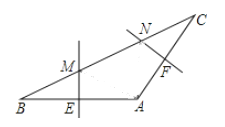
【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则AB长( )
A. ![]() B. 3 C. 2 D.
B. 3 C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com