
【题目】已知△ABC,∠BAC=45°,AB=8,要使满足条件的△ABC唯一确定,那么BC边长度x的取值范围为 .
【答案】x=4 ![]() 或x≥8
或x≥8
【解析】解:过B点作BD⊥AC于D点,则△ABD是等腰三角形;再延长AD到E,使DE=AD,
①当点C和点D重合时,△ABC是等腰直角三角形,BC=4 ![]() ,这个三角形是唯一确定的;
,这个三角形是唯一确定的;
②当点C和点E重合时,△ABC也是等腰三角形,BC=8,这个三角形也是唯一确定的;
③当点C在线段AE的延长线上时,即x大于BE,也就是x>8,这时,△ABC也是唯一确定的;
综上所述,∠BAC=45°,AB=8,要使△ABC唯一确定,那么BC的长度x满足的条件是:x=4 ![]() 或x≥8
或x≥8
【考点精析】掌握等腰直角三角形是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


科目:初中数学 来源: 题型:
【题目】如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD 
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.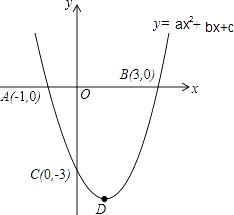
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com