
 中以点
中以点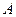 为圆心,
为圆心,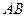 为半径作圆
为半径作圆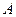 交网格于点
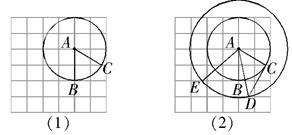
交网格于点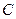 (如图(1)),过点
(如图(1)),过点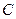 作圆的切线交网格于点
作圆的切线交网格于点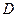 ,以点
,以点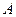 为圆心,
为圆心,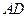 为半径作圆交网格于点
为半径作圆交网格于点
|
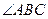 的度数;
的度数;
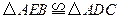 ;
;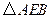 可以看作是由
可以看作是由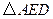 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断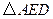 的形状(不用说明理由).
的形状(不用说明理由). 3),已知直线
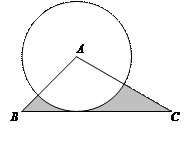
3),已知直线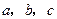 ,且a∥b,b∥c,在图中用
,且a∥b,b∥c,在图中用 直尺、三角板、圆规画等边三角形
直尺、三角板、圆规画等边三角形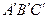 ,使三个顶点
,使三个顶点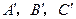 ,分别在直线
,分别在直线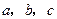 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
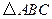 是等边三角形.……………………………………………2分
是等边三角形.……………………………………………2分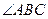 =60°;…………………………………………………………………………3分
=60°;…………………………………………………………………………3分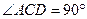
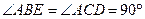 .…………………………………………………………………4分
.…………………………………………………………………4分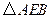 与Rt
与Rt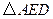 中,
中,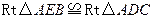 (HL).……………………………………………………6分
(HL).……………………………………………………6分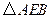 可以看作是由
可以看作是由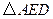 绕点A顺时针旋转60°得到的.…………7分
绕点A顺时针旋转60°得到的.…………7分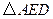 是等边三角形.………………………………………………………………8分
是等边三角形.………………………………………………………………8分

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
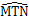 的度数( )
的度数( )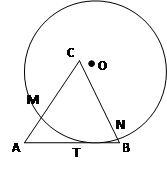
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com