练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在Rt△ABC中，∠C=90°，斜边c=5，两直角边的长a，b是关于x的一元二次方程的两个根，则Rt△ABC中较短的直角边长为__________.

    【答案】3

    【解析】

    根据一元二次方程的根与系数的关系求得m的值后，再求得方程的解.

    ∵a，b是方程x2-mx+2m-2=0的解，
    ∴a+b=m，ab=2m-2，
    在Rt△ABC中，由勾股定理得，a2+b2=c2，
    而a2+b2=（a+b）2-2ab，c=5，
    ∴a2+b2=（a+b）2-2ab=25，
    即：m2-2（2m-2）=25
    解得，m1=7，m2=-3，

    ∵a，b是Rt△ABC的两条直角边的长．
    ∴a+b=m＞0，m=-3不合题意，舍去．
    ∴m=7，
    当m=7时，原方程为x2-7x+12=0，
    解得，x1=3，x2=4，

    所以Rt△ABC的三条边分别为5、4、3,最小边为3.

    故答案是：3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

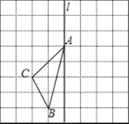
    【题目】如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．

    （1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；

    （2）△ABC的面积为　 　；

    （3）以AC为边作与△ABC全等的三角形，则可作出　 　个三角形与△ABC全等；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D，再分别以点C、D为圆心，大于CD的长为半径画弧，两弧在∠AOB内部交于点E，作射线OE，连接CD,以下说法错误的是（ ）

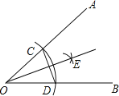
    A.△OCD是等腰三角形B.CD垂直平分OE

    C.点E到OA、OB的距离相等D.证明射线OE是角平分线的依据是SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程（x﹣3）（x﹣2）=|m|．

    （1）求证：对于任意实数m，方程总有两个不相等的实数根；

    （2）若方程的一个根是1，求m的值及方程的另一个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算下列各题：

    （1）（﹣1）2018+3﹣2﹣（π﹣3.14）0

    （2）（x+3）2﹣x2

    （3）（x+2）（3x﹣y）﹣3x（x+y）

    （4）（2x+y+1）（2x+y﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

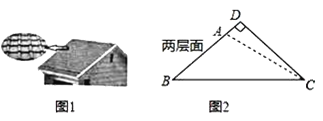
    【题目】太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）

    （参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列各组条件中，不能说明的是（ ）

    A.AB=DE，∠B=∠E，∠C=∠FB.AB=DE，∠A=∠D，∠B=∠E

    C.AC=DF，BC=EF，∠A=∠DD.AB=DE，BC=EF，AC=ED

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，点A，B分别在x，y轴上，点C是OB的中点，BE，CD都与x轴平行，BD⊥AB，∠ABO=30°．

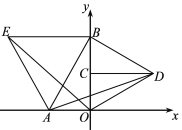
    （1）判断△OBD的形状；

    （2）若A（-3，0），BE=6，求证OE=AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填空并完成以下证明：

    已知：点P在直线CD上，∠BAP+∠APD=180°，∠1=∠2．

    求证：AB∥CD，∠E=∠F．

    证明：∵∠BAP+∠APD=180°，（已知）

    ∴AB∥　 　．（　 　）

    ∴∠BAP=　 　．（　 　）

    又∵∠1=∠2，（已知）

    ∠3=　 　﹣∠1，

    ∠4=　 　﹣∠2，

    ∴∠3=　 　（等式的性质）

    ∴AE∥PF．（　 　）

    ∴∠E=∠F．（　 　）

    查看答案和解析>>

    同步练习册答案