
 如图所示.点C、D在线段AB上,且点D是线段CB的中点.
如图所示.点C、D在线段AB上,且点D是线段CB的中点. 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. | 1,1+$\sqrt{2}$ | B. | 1,1-$\sqrt{2}$ | C. | -1,1+$\sqrt{2}$ | D. | -1,1-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
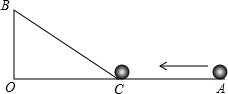 如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=25m,OB=5m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式,次数为1 | B. | 单项式,次数为2 | C. | 多项式,次数为2 | D. | 多项式,次数为3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com