
【题目】图1的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图.若图2中,∠AED=15°,则∠BCE的度数为何?( )

A. 30 B. 32.5 C. 35 D. 37.5
【答案】D
【解析】
根据直角三角形30°角所对的直角边等于斜边的一半可得△ABE、△A′BE皆为30°、60°、90° 的三角形,所以∠AEB=60°,再根据平角等于180°求出∠AED′=60°,即可求得∠DED′=75°,然后根据翻折变换的性质求出∠2=37.5°,再根据两直线平行,内错角相等解答.
如图,
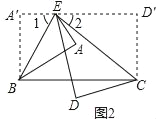
根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
∴△ABE、△A′BE皆为30°、60°、90° 的三角形,
∴∠1=∠AEB=60°,
∴∠AED′=180°﹣∠1﹣∠AEB=180°﹣60°﹣60°=60°,
∴∠DED′=∠AED+∠AED′=15°+60°=75°,
∴∠2=![]() ∠DED′=37.5°,
∠DED′=37.5°,
∵A′D′∥BC,
∴∠BCE=∠2=37.5°.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是定长线段
是定长线段![]() 上一定点,点
上一定点,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,点
上,点![]() 、点
、点![]() 分别从点
分别从点![]() 、点
、点![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.
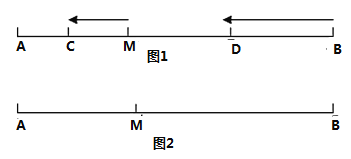
(1)若![]() ,当点C、D运动了2s,求
,当点C、D运动了2s,求![]() 的值;
的值;
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,直接填空:
,直接填空:![]() ______
______![]() ;
;
(3)在(2)的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
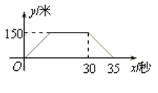
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
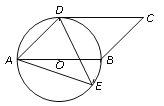
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
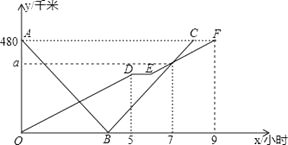
【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)求慢车的行驶速度和![]() 的值;
的值;
(2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
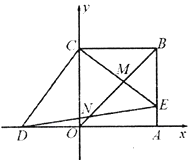
【题目】如图,在平面直角坐标系中,正方形![]() 两顶点为
两顶点为![]() ,
,![]() ,点D的坐标为
,点D的坐标为![]() ,在
,在![]() 上取点E,使得
上取点E,使得![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于M,N两点.
于M,N两点.
(1)求证:![]() ;
;
(2)求点E的坐标和线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在M,N两点中任选一点求出它的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com