
【题目】完成下列证明:
已知:AB//CD,连AD交BC于点F,∠1=∠2,求证:∠B+∠CDE=180°
证明:∵∠1= ( )
又∵∠1=∠2
∴∠BFD=∠2( )
∴BC// ( )
∴∠C+ =180°( )
又∵AB//CD
∴∠B=∠C( )
∴∠B+∠CDE=180°

【答案】∠BFD(对顶角相等),等量代换),ED,(同位角相等,两直线平行),∠CDE(两直线平行,同旁内角互补),(两直线平行,内错角相等)
【解析】
首先利用对顶角相等得∠1=∠BFD,等量代换得∠2=∠BFD,再利用平行线的判定定理和性质得解答即可.
证明:∵∠1= ∠BFD ( 对顶角相等 )
又∵∠1=∠2
∴∠BFD=∠2( 等量代换 )
∴BC// ED ( 同位角相等,两直线平行 )
∴∠C+ ∠CDE =180°( 两直线平行,同旁内角互补 )
又∵AB//CD
∴∠B=∠C( 两直线平行,内错角相等 )
∴∠B+∠CDE=180°.
故答案为:∠BFD(对顶角相等),(等量代换),ED(同位角相等,两直线平行),∠CDE,(两直线平行,同旁内角互补),(两直线平行,内错角相等).


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系XOY中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m//x轴,过点B作直线n//y轴,直线m、n相交于点 C.当线段AC、BC的长度相等时,称点B为点A的等距点,称△ABC的面积为点A的等距面积.
例如:如图,点A(2,1),点B(5,4),因为AC=BC=3,所以点B为点A的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-2,-2)中,点A的等距点为 ;
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,且点A的等距面积等于![]() ,求此时点B的坐标.
,求此时点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近一个月来我市遭受暴雨袭击,沱江水位上涨。小明以警戒水位为0点,用折线统计图表示某一天江水水位情况,请你结合折线统计图判断下列叙述不正确的是( )

A. 8时水位最高B. 8时到16时水位都在下降
C. 这一天水位均高于警戒水位D. P点表示12时水位高于警戒水位0.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的![]() ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 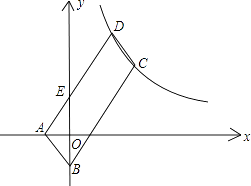
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为奖励在小运动会上取得较好成绩的运动员,花了400元钱购买甲、乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种奖品各买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AB为⊙O的直径,连结BD.若∠BCD=120°,则∠ABD的大小为( )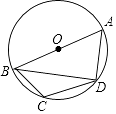
A.60°
B.50°
C.40°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形![]() 内,将两张边长分别为
内,将两张边长分别为![]() 和
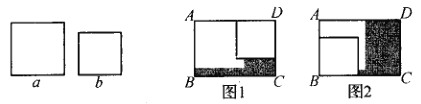
和![]() 的正方形纸片按如图,如图两种方式放置(如图,如图中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设如图1中阴影部分的面积为
的正方形纸片按如图,如图两种方式放置(如图,如图中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设如图1中阴影部分的面积为![]() ,如图2中阴影部分的面积为
,如图2中阴影部分的面积为![]() .当
.当![]() 时,
时,![]() 的值为( )
的值为( )
A. 0B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com