
【题目】对于平面直角坐标系XOY中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m//x轴,过点B作直线n//y轴,直线m、n相交于点 C.当线段AC、BC的长度相等时,称点B为点A的等距点,称△ABC的面积为点A的等距面积.
例如:如图,点A(2,1),点B(5,4),因为AC=BC=3,所以点B为点A的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-2,-2)中,点A的等距点为 ;
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,且点A的等距面积等于![]() ,求此时点B的坐标.
,求此时点B的坐标.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根据以上信息,解答下列问题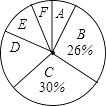
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,正确的有( )
①如果![]() ,那么
,那么![]() ;②满足条件
;②满足条件![]() 的n不存在;
的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C, ∠A-∠C=40°,则这个△ABC为钝角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有20个球,其中红球6个,白球和黑球若干个,每个球除颜色外完全相同.
(1)小明通过大量重复试验(每次将球搅匀后,任意摸出一个球,记下颜色后放回)发现,摸出的黑球的频率在0.4附近摆动,请你估计袋中黑球的个数.
(2)若小明摸出的第一个球是白球,不放回,从袋中余下的球中再任意摸出一个球,摸出白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:
已知:AB//CD,连AD交BC于点F,∠1=∠2,求证:∠B+∠CDE=180°
证明:∵∠1= ( )
又∵∠1=∠2
∴∠BFD=∠2( )
∴BC// ( )
∴∠C+ =180°( )
又∵AB//CD
∴∠B=∠C( )
∴∠B+∠CDE=180°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com