
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根据以上信息,解答下列问题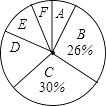
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
【答案】
(1)13,30
(2)50,18
(3)C
(4)解:调查家庭中不超过9.0吨的户数有:4+13+15=32,
![]() =128(户),
=128(户),
答:该月用水量不超过9.0吨的家庭数为128户
【解析】解:⑴观察表格可得4.0<x≤6.5的家庭有13户,6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比为30%;
⑵调查的家庭数为:13÷26%=50,
6.5<x≤9.0 的家庭数为:50×30%=15,
D组9.0<x≤11.5 的家庭数为:50﹣4﹣13﹣6﹣3﹣15=9,
9.0<x≤11.5 的百分比是:9÷50×100%=18%;
⑶调查的家庭数为50户,则中位数为第25、26户的平均数,从表格观察都落在C组;
故答案为:(1)13,30;(2)50,18;(3)C;
(1)观察表格和扇形统计图就可以得出结果;
(2)利用C组所占百分比及户数可算出调查家庭的总数,从而算出D组的百分比;
(3)从第二问知道调查户数为50,则中位数为第25、26户的平均数,由表格可得知落在C组;
(4)计算调查户中用水量不超过9.0吨的百分比,再乘以小区内的家庭数就可以算出.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为 , 设正方形的边长为a,则a= .
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如 ![]() =
= ![]() =
= ![]() .类比此,可以将(1)中的a表示成a= .
.类比此,可以将(1)中的a表示成a= .
(3)![]() =
= ![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为 ![]() ;类比此,(2)中的a可以理解为以长度和为直角边的直角三角形斜边的长.
;类比此,(2)中的a可以理解为以长度和为直角边的直角三角形斜边的长.
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成A、B、C、D、E五部分.
(5)拼一拼:把图②中五部分拼接得到如图③的正方形.
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在锐角![]() 中,
中,![]() ,AD⊥BC于D,在AD上取点E,使
,AD⊥BC于D,在AD上取点E,使![]() ,连结BE.求证:
,连结BE.求证:![]() .问题拓展:如图②,在问题原型的条件下,
.问题拓展:如图②,在问题原型的条件下,![]() 为
为![]() 的中点,连结
的中点,连结![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连结
,连结![]() .
.
图① 图②
图②
(1)判断线段![]() 与
与![]() 的大小关系,并说明理由.(2)若
的大小关系,并说明理由.(2)若![]() ,直接写出
,直接写出![]() 、
、![]() 两点之间的距离.
两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )![]()
A.ac>bc
B.|a﹣b|=a﹣b
C.﹣a<﹣b<c
D.﹣a﹣c>﹣b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系XOY中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m//x轴,过点B作直线n//y轴,直线m、n相交于点 C.当线段AC、BC的长度相等时,称点B为点A的等距点,称△ABC的面积为点A的等距面积.
例如:如图,点A(2,1),点B(5,4),因为AC=BC=3,所以点B为点A的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-2,-2)中,点A的等距点为 ;
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,且点A的等距面积等于![]() ,求此时点B的坐标.
,求此时点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.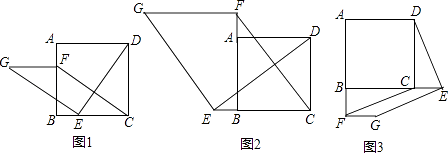
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑩个图形中平行四边形的个数为( )

 ……
……
图① 图② 图③ 图④
A. 108B. 109C. 110D. 111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 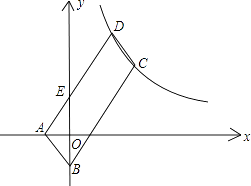
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com