
【题目】问题原型:如图①,在锐角![]() 中,
中,![]() ,AD⊥BC于D,在AD上取点E,使
,AD⊥BC于D,在AD上取点E,使![]() ,连结BE.求证:
,连结BE.求证:![]() .问题拓展:如图②,在问题原型的条件下,
.问题拓展:如图②,在问题原型的条件下,![]() 为
为![]() 的中点,连结
的中点,连结![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连结
,连结![]() .
.
图① 图②
图②
(1)判断线段![]() 与
与![]() 的大小关系,并说明理由.(2)若
的大小关系,并说明理由.(2)若![]() ,直接写出
,直接写出![]() 、
、![]() 两点之间的距离.
两点之间的距离.
【答案】问题原型:见解析;(1)![]() ,见解析;(2)
,见解析;(2)![]() .
.
【解析】
问题原型:由AD⊥BC可得∠ADB=∠ADC=90°,又∠ABC=45°可得∠ABC=∠BAD,可得AD=BD,根据SAS定理可得△BDE≌△ADC;
问题拓展:(1)利用SAS判断出△BEF≌△CMF,得出BE=CM,即可得出结论;
(2)借助问题原型与问题延伸的结论判断出△ACM是等腰直角三角形,即可得出结论.
解:问题原型:∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ;
;
问题拓展:(1)![]() .
.
理由:∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ;
;
(2)如图②,
图②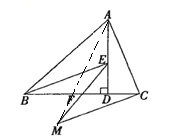
连接AM,由(1)知,△BDE≌△ADC,
∴∠BED=∠ACD,
由(2)知,△BEF≌△CMF,
∴∠EBF=∠BCM,
∴∠ACM=∠ACD+∠BCM=∠BED+∠EBF=90°,
∵AC=CM,
∴AM=![]() AC=4
AC=4![]() .
.
故答案为:(1)![]() ,见解析;(2)
,见解析;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,公路上距A处45千米的红方在B处沿南偏西67°方向前进实施拦截.红方行驶26千米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西37°方向前进,刚好在D处成功拦截蓝方.求拦截点D处到公路的距离AD.
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,sin37°≈
,sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉揭示了二项和![]() 的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
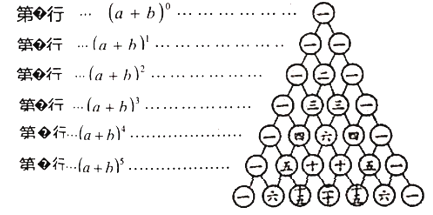
(1)观察“杨辉三角”规律,依次写出“杨辉三角”第![]() 行中从左到右的各数;
行中从左到右的各数;
(2)请运用幂的意义和多项式乘法法则,按如下要求展开下列各式,以验证“杨辉三角”第四行的规律:展开后各项按字母![]() 降幂、
降幂、![]() 升幂排列
升幂排列![]()
(3)解不等式![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>14.0 | 3 |
根据以上信息,解答下列问题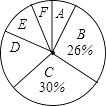
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,正确的有( )
①如果![]() ,那么
,那么![]() ;②满足条件
;②满足条件![]() 的n不存在;
的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C, ∠A-∠C=40°,则这个△ABC为钝角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com