
【题目】如图,以O为圆心的圆与直线y=﹣x+ ![]() 交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
A.![]() π
π
B.π
C.![]() π
π
D.![]() π
π
【答案】C
【解析】解:如图,作OC⊥AB于C,设AB与x轴交于点M,与y轴交于点N.
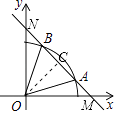
∵直线AB的解析式为y=﹣x+ ![]() ,
,
∴M( ![]() ,0),N(0,
,0),N(0, ![]() ),
),
∴OM=ON= ![]() ,△OMN是等腰直角三角形,
,△OMN是等腰直角三角形,
∴∠OMN=∠ONM=45°,
∵OC⊥AB,
∴OC= ![]() OM=
OM= ![]() .
.
∵△OAB为等边三角形,OC⊥AB,
∴AB=2AC,AC= ![]() =
= ![]() =
= ![]() ,∠AOB=60°,OA=OB=AB,
,∠AOB=60°,OA=OB=AB,
∴AB= ![]() ,
,
∴弧AB的长度为: ![]() =
= ![]() π.
π.
所以答案是:C.
【考点精析】通过灵活运用等边三角形的性质和弧长计算公式,掌握等边三角形的三个角都相等并且每个角都是60°;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在锐角![]() 中,
中,![]() ,AD⊥BC于D,在AD上取点E,使
,AD⊥BC于D,在AD上取点E,使![]() ,连结BE.求证:
,连结BE.求证:![]() .问题拓展:如图②,在问题原型的条件下,
.问题拓展:如图②,在问题原型的条件下,![]() 为
为![]() 的中点,连结
的中点,连结![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连结
,连结![]() .
.
图① 图②
图②
(1)判断线段![]() 与
与![]() 的大小关系,并说明理由.(2)若
的大小关系,并说明理由.(2)若![]() ,直接写出
,直接写出![]() 、
、![]() 两点之间的距离.
两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑩个图形中平行四边形的个数为( )

 ……
……
图① 图② 图③ 图④
A. 108B. 109C. 110D. 111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近一个月来我市遭受暴雨袭击,沱江水位上涨。小明以警戒水位为0点,用折线统计图表示某一天江水水位情况,请你结合折线统计图判断下列叙述不正确的是( )

A. 8时水位最高B. 8时到16时水位都在下降
C. 这一天水位均高于警戒水位D. P点表示12时水位高于警戒水位0.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的![]() ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 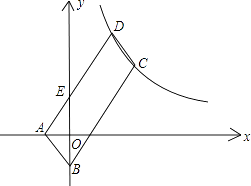
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AB为⊙O的直径,连结BD.若∠BCD=120°,则∠ABD的大小为( )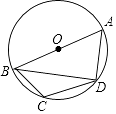
A.60°
B.50°
C.40°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB//CD,分别探究下列三个图形中∠APC和∠PAB,∠PCD的关系.

结论:(1)__________________________
(2)__________________________
(3)__________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com