
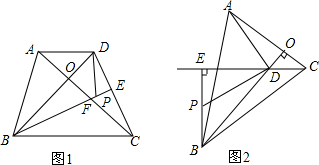
分析 (1)根据垂直的定义得到∠COD=∠BED=90°,根据三角形的内角和得到∠DBP=∠ACD,推出△ACD≌△DBP,根据全等三角形的性质得到AD=PD,∠DAC=∠DBP,根据余角的性质得到即可得到结论;
(2)根据垂直的定义得到∠COD=∠BED=90°,根据三角形的内角和得到∠DBP=∠ACD,推出△ACD≌△DBP,根据全等三角形的性质得到AD=PD,∠DAC=∠DBP,根据余角的性质得到即可得到结论.
解答 解:(1)AD=PD,AD⊥PD,
理由:∵AC⊥BD,BE⊥CD,
∴∠COD=∠BED=90°,
∵∠ODE=∠ODE,
∴∠DBP=∠ACD,
在△ACD与△BDP中,$\left\{\begin{array}{l}{AC=BD}\\{∠ACD=∠DBP}\\{CD=BP}\end{array}\right.$,
∴△ACD≌△DBP,
∴AD=PD,∠DAC=∠DBP,
∵∠DAC+∠ADB=90°,
∴∠ADB+∠BDP=90°,
∴∠ADP=90°,
∴AD⊥DP;
(2)(1)中的结论成立,
∵AC⊥BD,BE⊥CD,
∴∠COD=∠BED=90°,
∵∠ODE=∠ODE,
∴∠DBP=∠ACD,
在△ACD与△BDP中,$\left\{\begin{array}{l}{AC=BD}\\{∠ACD=∠DBP}\\{CD=BP}\end{array}\right.$,
∴△ACD≌△DBP,
∴AD=PD,∠DAC=∠DBP,
∵∠DAC+∠ADB=90°,
∴∠ADB+∠BD=90°,
∴∠ADP=90°,
∴AD⊥DP.
点评 本题考查了全等三角形的判定和性质,三角形的内角和,余角的性质,熟练掌握全等三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
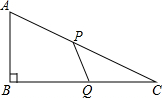 如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒.
如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
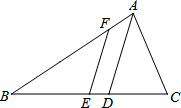 如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.
如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
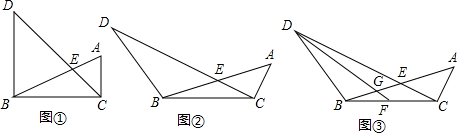
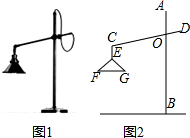 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com