
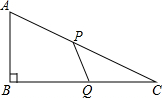
 ��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮
��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮���� ��1��ͼ1�У���PD��BC��D��������������λ�߶����������PD�ij���Ȼ�����������ε������ʽ������⣮
��2��ͼ1�У���QE��PC�ڵ�E������Rt��QEC��Rt��ABC���QE���ɣ�
��3����������������ۢ�PC=QC ��PQ=QC ��PC=PQ���ֱ��г����̼��ɽ����
��� �⣺��Rt��ABC�У�AB=6�ף�BC=8�ף���AC=10��
������ã�AP=2t����CQ=t����PC=10-2t��
��1��ͼ1�У���PD��BC��D��
��t=2.5��ʱ��AP=2��2.5=5�ף�QC=2.5�ף�
��PA=PC��
�ߡ�PDC=��B=90�㣬
��PD��AB��
��PD=$\frac{1}{2}$AB=3�ף���S=$\frac{1}{2}$•QC•PD=3.75ƽ���ף�
��2��ͼ1�У���QE��PC�ڵ�E��
���C=��C����QEC=��B=90��
��Rt��QEC��Rt��ABC��
��$\frac{QE}{QC}$=$\frac{AB}{AC}$��
��ã�QE=$\frac{3}{5}t$��
��S=$\frac{1}{2}$•PC•QE=$\frac{1}{2}$•��10-2t��•$\frac{3}{5}t$=-$\frac{3}{5}$t2+3t��0��t��5�� ��3���ߡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�
��3���ߡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��PC=QCʱ��PC=10-2t��QC=t����10-2t=t�����t=$\frac{10}{3}$�룻
��PQ=CQʱ����ͼ1������Q��QE��AC����CE=$\frac{10-2t}{2}$=5-t��CQ=t��
�ɡ�CEQ�ס�CBA����$\frac{CE}{BC}=\frac{QC}{AC}$����$\frac{5-t}{8}=\frac{t}{10}$�����t=$\frac{25}{9}$�룻
��PC=PQʱ����ͼ2������P��PE��BC����CE=$\frac{t}{2}$��PC=10-2t��
�ɡ�PCE�ס�ACB���ʵ�$\frac{CE}{BC}$=$\frac{PC}{AC}$����$\frac{\frac{t}{2}}{8}=\frac{10-2t}{10}$�����t=$\frac{80}{21}$��
���Ե�t=$\frac{10}{3}$�루��ʱPC=QC����$\frac{25}{9}$�루��ʱPQ=QC������$\frac{80}{21}$�루��ʱPQ=PC����CPQΪ���������Σ�
���� ������Ҫ���������������ε����ʡ����ɶ��������������ε����ʡ��������������ε������ǽ���Ĺؼ���ѧ��ת����˼�룬������ת��Ϊ���̽���������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a3=a9 | B�� | ��a3��2=a5 | C�� | ��2ab2��3=6a3b6 | D�� | ��-a��7�£�-a��2=-a5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
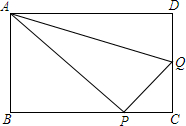 ��ͼ���ھ���ABCD�У�AB=6cm��BC=8cm������P��B�㿪ʼ�ر�BC���C��4cm/s���ٶ��˶���ͬʱ����Q��C�㿪ʼ�ر�CD���D��1cm/s���ٶ��˶���������һ�������յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
��ͼ���ھ���ABCD�У�AB=6cm��BC=8cm������P��B�㿪ʼ�ر�BC���C��4cm/s���ٶ��˶���ͬʱ����Q��C�㿪ʼ�ر�CD���D��1cm/s���ٶ��˶���������һ�������յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
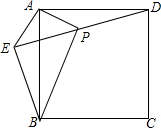 ��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=$\sqrt{6}$�����н��ۣ�
��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=$\sqrt{6}$�����н��ۣ�| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �ڢۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
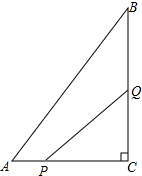 ��ͼ���ڡ�ABC�У���C=90�㣬AC=6cm��BC=8cm����P��A�㿪ʼ��AC�����C��1cm/s���ٶ��˶�����C��ֹͣ����Q��C�㿪ʼ��CB�������B��2cm/s���ٶ��˶����ڵ�Bֹͣ�������P��Q�ֱ��A��Cͬʱ�������������룬��PCQ�������8cm2��
��ͼ���ڡ�ABC�У���C=90�㣬AC=6cm��BC=8cm����P��A�㿪ʼ��AC�����C��1cm/s���ٶ��˶�����C��ֹͣ����Q��C�㿪ʼ��CB�������B��2cm/s���ٶ��˶����ڵ�Bֹͣ�������P��Q�ֱ��A��Cͬʱ�������������룬��PCQ�������8cm2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com