
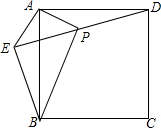
 ��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=$\sqrt{6}$�����н��ۣ�
��ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=$\sqrt{6}$�����н��ۣ�| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �ڢۢ� | D�� | �٢ڢ� |
���� ������ͬ�ǵ������ȣ��á�EAB=��PAD���ٽ����֪��������SAS��֤��������ȫ�ȣ������â��е�ȫ�ȣ��ɵá�APD=��AEB����������ε���ǵ����ʣ��á�BEP=90�㣬����֤���ڹ�B��BF��AE����AE���ӳ�����F�����â��еġ�BEP=90�㣬���ù��ɶ�������BE����ϡ�AEP�ǵ���ֱ�������Σ���֤��BEF�ǵ���ֱ�������Σ������ù��ɶ�������EF��BF������Rt��ABF�У����ù��ɶ�������AB2�����������ε������������BD�������ABD�������Ȼ���ȥ��BDP��������ɣ�
��� �⣺�١ߡ�EAB+��BAP=90�㣬��PAD+��BAP=90�㣬
���EAB=��PAD��
�ڡ�APD�͡�AEB��
$\left\{\begin{array}{l}{AP=AE}\\{��PAD=��EAB}\\{AD=AB}\end{array}\right.$
���APD�ա�AEB��SAS�����ʢ���ȷ����
�ۡߡ�APD�ա�AEB��
���APD=��AEB��
�֡ߡ�AEB=��AEP+��BEP����APD=��AEP+��PAE��
���BEP=��PAE=90�㣬
��EB��ED���ʢ���ȷ����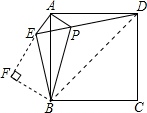
�ڹ�B��BF��AE����AE���ӳ�����F��
��AE=AP����EAP=90�㣬
���AEP=��APE=45�㣬
�֡ߢ���EB��ED��BF��AF��
���FEB=��FBE=45�㣬
�֡�BE=$\sqrt{B{P}^{2}-P{E}^{2}}$=2��
��BF=EF=$\sqrt{2}$���ʢڲ���ȷ����
����ͼ������BD����Rt��AEP�У�
��AE=AP=1��
��EP=$\sqrt{2}$��
�֡�PB=$\sqrt{6}$��
��BE=2��
�ߡ�APD�ա�AEB��
��PD=BE=2��
��S��ABP+S��ADP=S��ABD-S��BDP=$\frac{1}{2}$S������ABCD-$\frac{1}{2}$��DP��BE=$\frac{1}{2}$����2+3+2$\sqrt{2}$��-$\frac{1}{2}$��2��2=$\frac{1}{2}$+$\sqrt{2}$�����ʢܲ���ȷ����
�ݡ�EF=BF=$\sqrt{2}$��AE=1��
����Rt��ABF��AB2=��AE+EF��2+BF2=3+2$\sqrt{2}$+2=5+2$\sqrt{2}$��
��S������ABCD=AB2=5+2$\sqrt{2}$���ʢ���ȷ����
��ѡ��B��
���� ����������ȫ�������ε��ж������ʡ������ε����ʡ������κ������ε������ʽ�����ɶ�����֪ʶ���ۺ��ԱȽ�ǿ���ó���APD�ա�AEB���������ȫ�������ε����ʷ����ǽ���ؼ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
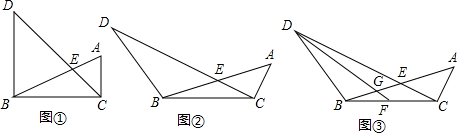
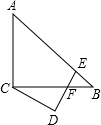 ��ͼ����ABC�У���ACB=90�㣬AC=BC��EΪAB��һ�㣬��CDE=90�㣬��CD=DE��DE��BC�ڵ�F������BCD=30�㣬AB=4$\sqrt{3}$����DF�ij�Ϊ$\frac{2\sqrt{6}}{3}$��
��ͼ����ABC�У���ACB=90�㣬AC=BC��EΪAB��һ�㣬��CDE=90�㣬��CD=DE��DE��BC�ڵ�F������BCD=30�㣬AB=4$\sqrt{3}$����DF�ij�Ϊ$\frac{2\sqrt{6}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
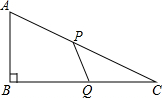 ��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮
��ͼ���ڡ�ABC�У���B=90�㣬AB=6�ף�BC=8�ף�����P��2��/����ٶȴ�A���������AC���C�ƶ���ͬʱ������Q��1��/����ٶȴ�C���������CB���B�ƶ�����������һ�㵽���յ�ʱ�����Ƕ�ֹͣ�����ƶ���ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
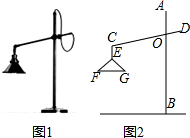 ��ͼ1��ʾ����һ�����������ϵļ���̨�ƣ�����ṹ��ͼ2���Ƹ�AB��CD���ڵ�O����O�̶�������������CEʼ�ձ�����ABƽ�У������·�FG����ˮƽλ�ã����OC=20cm����COB=70�㣬��F=40�㣬EF=EG����G��OB�ľ���Ϊ12cm��
��ͼ1��ʾ����һ�����������ϵļ���̨�ƣ�����ṹ��ͼ2���Ƹ�AB��CD���ڵ�O����O�̶�������������CEʼ�ձ�����ABƽ�У������·�FG����ˮƽλ�ã����OC=20cm����COB=70�㣬��F=40�㣬EF=EG����G��OB�ľ���Ϊ12cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
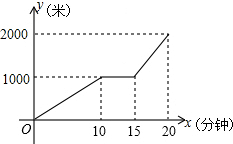 ij��С�������г��Ӽҳ���ȥѧУ��ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ����С������������ʱ��Ϊx�����ӣ�����ҵľ���Ϊy���ף���y��x�ĺ����Ĵ���ͼ����ͼ��ʾ������˵��������ǣ�������
ij��С�������г��Ӽҳ���ȥѧУ��ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ����С������������ʱ��Ϊx�����ӣ�����ҵľ���Ϊy���ף���y��x�ĺ����Ĵ���ͼ����ͼ��ʾ������˵��������ǣ�������| A�� | �ҵ�ѧУ�ľ�����2000�� | |
| B�� | �������ʱ����5���� | |
| C�� | �������г����ٶ���ÿ����200�� | |
| D�� | ��ǰ�������ٶȿ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 56 | B�� | 34 | C�� | 28 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
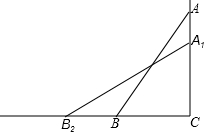 ��ͼ��һ��2.5�׳�������ABб������ֱ��ǽAC�ϣ���ʱ���ӵײ�B��ǽ�˵ľ���Ϊ0.7�ף����������ӵ��ȶ��ԣ���Ҫ�����Ӷ���A��ǽ����0.4��A1���������ӵײ�B�����ƶ����ף�
��ͼ��һ��2.5�׳�������ABб������ֱ��ǽAC�ϣ���ʱ���ӵײ�B��ǽ�˵ľ���Ϊ0.7�ף����������ӵ��ȶ��ԣ���Ҫ�����Ӷ���A��ǽ����0.4��A1���������ӵײ�B�����ƶ����ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com