
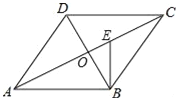
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求线段OE的长.
,求线段OE的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:本题考查了解直角三角形及菱形的判定与性质、平行四边变形的判定与性质的知识,解题的关键是读懂题意,选择合适的边角关系,难度不大.(1)、根据∠CAB=∠ACB利用等角对等边得到AB=CB,从而判定平行四边形ABCD是菱形,根据菱形的对角线互相垂直即可证得结论;(2)、分别在Rt△AOB中和在Rt△ABE中求得AO和AE,从而利用OE=AE﹣AO求解即可.
试题解析:(1)∵∠CAB=∠ACB, ∴AB=CB, ∴ABCD是菱形. ∴AC⊥BD;
(2)在Rt△AOB中,cos∠CAB=![]() =
=![]() ,AB=14, ∴AO=14×
,AB=14, ∴AO=14×![]() =
=![]() ,
,
在Rt△ABE中,cos∠EAB=![]() =
=![]() ,AB=14, ∴AE=
,AB=14, ∴AE=![]() AB=16, ∴OE=AE﹣AO=16﹣
AB=16, ∴OE=AE﹣AO=16﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
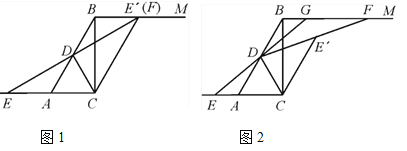
【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2![]() ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
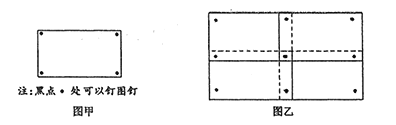
【题目】某班在一块展示板上同时展示形状与大小均相同的长方形(图甲)的班徽设计作品,并将这些作品排成一个长方形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在展示板上,如图乙所示).若有38枚图钉可供选用,则最多可以展示设计作品件数( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com