
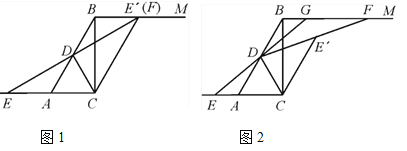
【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2![]() ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2) ①y=![]() ;②
;②![]()
【解析】分析:(1)由翻折的性质得到∠ACD=∠E′CD,再由△ACD为等边三角形,得到∠ADC=∠ACD,由等量代换得到∠ADC=∠DCE′,进而得到AB∥CE′,即可得到结论.
(2)①解Rt△ABC得到AB=4, BD=2,再证明△BDG∽△BFD, 得到![]() ,即可得到结论.
,即可得到结论.
②由△BDG≌△ADE,得到BG=AE=x.过点D作DH⊥BM于点H,易得DH的长.
由S△DFG=![]() GF·DH,得到GF的长 ,解方程即可得到结论.
GF·DH,得到GF的长 ,解方程即可得到结论.
详解:(1)由翻折得∠ACD=∠E′CD.在Rt△ABC中,∵D为AB的中点,∴AD=CD.
又∵∠BAC=60°,∴△ACD为等边三角形,∴∠ADC=∠ACD,∴∠ADC=∠DCE′,
∴AB∥CE′.
又∵AC∥BE′,∴四边形ABE′C为平行四边形.
(2)①在Rt△ABC中,∵BC=2![]() ,∠BAC=60°,∴AB=4,∴BD=2.
,∠BAC=60°,∴AB=4,∴BD=2.
又∵BM∥CE,∴∠BGD=∠DEC,
由翻折得:∠DEC=∠DE′C.
又∵AB∥CE′,∴∠DE′C=∠BDF,∴∠BGD=∠BDF,
∴△BDG∽△BFD, ∴![]() ,
,
∴4=x(x+y),∴y=![]() .
.
②易证△BDG≌△ADE,∴BG=AE=x.
过点D作DH⊥BM于点H.
∵D为AB的中点,可得DH=![]() BC=
BC=![]() .
.
∵S△DFG=![]() GF·DH=3
GF·DH=3![]() ,∴GF=6 ,
,∴GF=6 ,
∴![]() =6,∴x=
=6,∴x=![]() .
.
又∵x>0,∴x=![]() ,∴AE=
,∴AE=![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】一次期中考试中,甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示:(单位:分)
甲 | 乙 | 丙 | 丁 | 戍 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分 的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看, 标准分大的考试成绩更好.请问甲同学在本次考试中,数学与英语哪个学科考 得更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从这两组中随机选取2名选手进行调研座谈,请用画树状图或列表法求第一组至少有1名选手被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b交x轴于点A(1,0),与双曲线y=-![]() (x<0)交于点B(-1,a).
(x<0)交于点B(-1,a).
(1)求直线AB的解析式;
(2)若点B左侧一直线x=m与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC=BD时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
今年A,B两种型号车的进价和售价如下表:
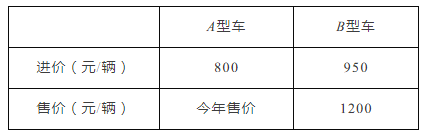
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
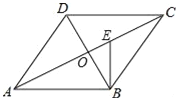
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求线段OE的长.
,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
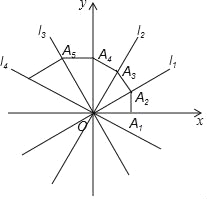
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
x,l4:y4=﹣![]() ,OA1=l,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l3交y轴于点A4…,则点A2坐标为_____;点A2018的坐标为_____.
,OA1=l,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l3交y轴于点A4…,则点A2坐标为_____;点A2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小江家的住房户型结构图.根据结构图提供的信息,解答下列问题:
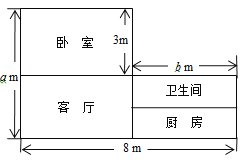
(1)用含a、b的代数式表示小江家的住房总面积S;
(2)小江家准备给房间重新铺设地砖.若卧室所用的地砖价格为每平方米50元;卫生间、厨房和客厅所用的地砖价格为每平方米40元.请用含a、b的代数式表示铺设地砖的总费用W;
(3)在(2)的条件下,当a=6,b=4时,求W的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com