
【题目】某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
今年A,B两种型号车的进价和售价如下表:
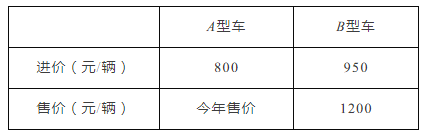
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
【答案】(1)![]() 型车每辆售价为1000元;(2)
型车每辆售价为1000元;(2)![]() 型车30辆、
型车30辆、![]() 型车20辆,获利最多.
型车20辆,获利最多.
【解析】
(1)设今年![]() 型车每辆售价为
型车每辆售价为![]() 元,则去年
元,则去年![]() 型车每辆售价为
型车每辆售价为![]() 元,根据数量
元,根据数量![]() 总价
总价![]() 单价结合今年6月份与去年同期相比销售数量相同,即可得出关于
单价结合今年6月份与去年同期相比销售数量相同,即可得出关于![]() 的分式方程,解之经检验后即可得出结论;
的分式方程,解之经检验后即可得出结论;
(2)设购进![]() 型车
型车![]() 辆,则购进
辆,则购进![]() 型车
型车![]() 辆,根据总价
辆,根据总价![]() 单价
单价![]() 数量结合总费用不超过4.3万元,即可得出关于
数量结合总费用不超过4.3万元,即可得出关于![]() 的一元一次不等式,解之即可得出
的一元一次不等式,解之即可得出![]() 的取值范围,再根据销售利润
的取值范围,再根据销售利润![]() 单辆利润
单辆利润![]() 购进数量即可得出销售利润关于
购进数量即可得出销售利润关于![]() 的函数关系式,利用一次函数的性质解决最值问题即可.
的函数关系式,利用一次函数的性质解决最值问题即可.
解:(1)设今年![]() 型车每辆售价为
型车每辆售价为![]() 元,则去年
元,则去年![]() 型车每辆售价为
型车每辆售价为![]() 元,
元,
根据题意得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原分式方程的解.
是原分式方程的解.
答:今年![]() 型车每辆售价为1000元.
型车每辆售价为1000元.
(2)设购进![]() 型车
型车![]() 辆,则购进
辆,则购进![]() 型车
型车![]() 辆,
辆,
根据题意得:![]() ,
,
解得:![]() .
.
销售利润为![]() ,
,
![]() ,
,
![]() 当
当![]() 时,销售利润最多.
时,销售利润最多.
答:当购进![]() 型车30辆、购进
型车30辆、购进![]() 型车20辆时,才能使这批车售完后获利最多.
型车20辆时,才能使这批车售完后获利最多.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:![]() 单位:千米
单位:千米![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 问收工时离出发点A多少千米?
问收工时离出发点A多少千米?
![]() 若该出租车每千米耗油
若该出租车每千米耗油![]() 升,问从A地出发到收工共耗油多少升?
升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校一教学楼高AB=15米,在它的正前方有一旗杆EF,从教学楼顶端A测得旗杆顶端E的俯角为30°,旗杆低端F到大楼前梯坎底边的距离CF=12米,梯坎坡长BC=6.5米,梯坎坡度i=1:2.4,求旗杆EF的高度.(结果保留根号)
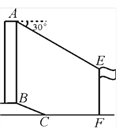
查看答案和解析>>
科目:初中数学 来源: 题型:
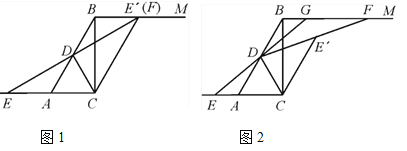
【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2![]() ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旗县开展2018美丽乡村美化绿化活动,小康村计划购买垂柳和丁香两种花木共100棵绿化村里的小广场,其中垂柳每棵50元,丁香每棵100元.
(1)若购进垂柳,丁香两种花木刚好用去8000元,则购买了垂柳,丁香两种花木各多少棵?
(2)如果购买丁香的数量不少于垂柳的数量,请你设计一种购买方案,使所需总费用最低,并求出该购买方案所需总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定理中,没有逆定理的是( )
A. 直角三角形的两锐角互余
B. 全等三角形的对应角相等
C. 互为相反数的两数之和为 0
D. 若三角形的三边长 a, b, c 满足 ![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b都表示有理数,规定一种新运算“Δ”:当a≥b时,aΔb=b2;当a<b时,aΔb=2a.例如:1Δ2=2×1=2;3Δ(-2)=(-2)2=4.
![]()
(1) (-3)Δ(-4) = ;
(2)求(2Δ3)Δ(-5);
(3)若有理数x在数轴上对应点的位置如图所示,求 (1Δx)Δx-(3Δx).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com