
【题目】如图,直线y=kx+b交x轴于点A(1,0),与双曲线y=-![]() (x<0)交于点B(-1,a).
(x<0)交于点B(-1,a).
(1)求直线AB的解析式;
(2)若点B左侧一直线x=m与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC=BD时,求m的值.

【答案】(1) y=-x+1 ;(2) m=-2.
【解析】分析:(1)由点B(-1,a)在双曲线上,可得B的坐标.再由直线y=kx+b过点A、B,可得直线AB的解析式.
(2)过点B作BE⊥CD于点E.由等腰三角形的性质得到DE=CE=![]() CD,由C(m,-m+1),D(m,-
CD,由C(m,-m+1),D(m,-![]() ),得到CD=-m+1+
),得到CD=-m+1+![]() ,故
,故![]() (-m+1+
(-m+1+![]() )-
)-![]() =2,解方程即可得到结论.
=2,解方程即可得到结论.
详解:(1)∵点B(-1,a)在双曲线上,∴a=2,∴B(-1,2).
又∵直线y=kx+b过点A、B,故得:![]() ,
,
解得:![]() ,∴直线AB的解析式为:y=-x+1 .
,∴直线AB的解析式为:y=-x+1 .
(2)过点B作BE⊥CD于点E.
∵BC=BD, ∴DE=CE=![]() CD,
CD,
由题意可知,C(m,-m+1),D(m,-![]() ),
),
∴CD=-m+1+![]() ,
,
∴![]() (-m+1+
(-m+1+![]() )-
)-![]() =2,
=2,
∴m=-1或-2.
又∵m<-1,∴m=-2.


科目:初中数学 来源: 题型:
【题目】完成下列填空:
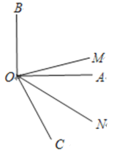
(1)如图,![]() 为直角,
为直角,![]() ,且
,且![]() 平分
平分![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.
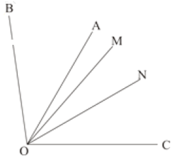
(2)如图,![]() ,且
,且![]() 平分
平分![]() 平分
平分![]() .直接写出
.直接写出![]() 的度数.
的度数.
解:(1)因为![]() ,所以
,所以![]() ①
① ![]()
因为![]() 平分
平分![]() ,所以
,所以![]() ②
② ![]() ③
③ ![]()
因为![]() 平分
平分![]() ,所以
,所以![]() ④
④ ![]() ⑤
⑤ ![]()
所以![]() ⑥
⑥ ![]()
(2)![]() ⑦
⑦ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+x2>2,则y1> y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为![]() .其中正确判断的序号是( )
.其中正确判断的序号是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售![]() 元,在果园每千克售
元,在果园每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用![]() 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
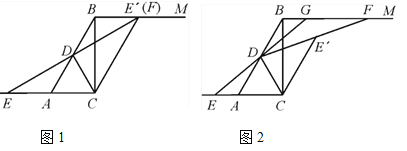
【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2![]() ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
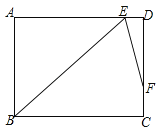
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com