
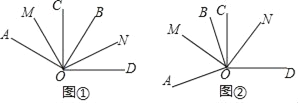
【题目】如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
【答案】(1)∠MON=90°;(2)∠MON=90°;(3)∠MON=90°.
【解析】
(1)由∠AOB=∠COD=90°,∠BOC=20°,可得∠MOC=∠BON的度数,可得∠MON的度数:
(2)同理由∠AOB=∠COD=90°,∠BOC=α,可得∠MOC=∠BON的度数,可得∠MON的度数:
(3)由∠AOB=∠COD=90°,∠BOC=α,可得∠AOC=∠BOD=90°+α,∠MOC=∠BON=45°+![]() α可得∠MON的度数:
α可得∠MON的度数:
解:
(1)∵∠AOB=∠COD=90°,∠BOC=20°,
∴∠AOC=∠BOD=90°﹣20°=70°.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=35°,
∴∠MON=∠MOC+∠COB+∠BON=35°+20°+35°=90°;
(2)∵∠AOB=∠COD=90°,∠BOC=α,
∴∠AOC=∠BOD=90°﹣α.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=45°﹣![]() α,
α,
∴∠MON=∠MOC+∠COB+∠BON=45°﹣![]() α+α+45°﹣
α+α+45°﹣![]() =90°;
=90°;
(3)∵∠AOB=∠COD=90°,∠BOC=α,
∴∠AOC=∠BOD=90°+α.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=45°+![]() α,
α,
∴∠MON=∠MOC﹣∠COB+∠BON=45°+![]() α﹣α+45°+
α﹣α+45°+![]() =90°.
=90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下: 5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表: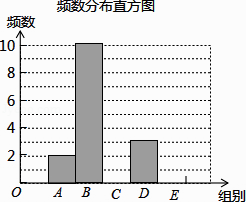
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)求m,n的值;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和小明值日打扫教室卫生,小玲单独打扫雪20min完成,小明单独打扫雪16min完成.因小明要将数学作业本交到老师办公室推迟一会儿,故先由小玲单独打扫4min,余下的再由两人一起完成,则两人一起打扫完教师卫生需要多长时间?设两人一起打扫完教室卫生需要x min,则根据题意可列方程( )
A. ![]() (x+4)+
(x+4)+![]() x=1 B.
x=1 B. ![]() x+
x+![]() (x+4)=1
(x+4)=1
C. ![]() (x﹣4)+
(x﹣4)+![]() x=1 D.
x=1 D. ![]() x+
x+![]() (x﹣4)=1
(x﹣4)=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 与坐标原点重合,点
与坐标原点重合,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,一次函数
,一次函数![]() 的图象过点
的图象过点![]() 和
和![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,且与
,且与![]() 的交点为
的交点为![]() .
.
(1)直接写出反比例函数解析式 一次函数的解析式 ;
(2)若点![]() 在直线
在直线![]() 上,且使△OPM的面积与四边形
上,且使△OPM的面积与四边形![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两材料,并解决相关的问题.
(材料一)按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为![]() ,依此类推,排在第
,依此类推,排在第![]() 位的数称为第
位的数称为第![]() 项,记为
项,记为![]() .一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母
.一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母![]() 表示
表示![]() ,如数列
,如数列![]() 为等比数列,其中
为等比数列,其中![]() ,公比
,公比![]() .
.
(材料二)为了求![]() 的值.可令
的值.可令![]()
则![]() , 因此
, 因此![]() ,所以
,所以![]() ,
,
即![]()
(1)等比数列![]() 的公比
的公比![]() 为_________,第6项是________
为_________,第6项是________
(2)如果一个数列![]() 是等比数列,且公比为
是等比数列,且公比为![]() ,那么根据定义可得到
,那么根据定义可得到![]() ,
,![]() ,
,![]() ,由此可得
,由此可得![]() (用
(用![]() 和
和![]() 的代数式表示)
的代数式表示)
(3)若某等比数列的公比![]() ,第2项
,第2项![]() ,则它的第1项
,则它的第1项![]() ,第4项
,第4项![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).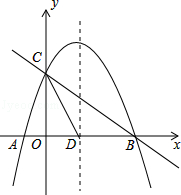
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com