
【题目】阅读下列两材料,并解决相关的问题.
(材料一)按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为![]() ,依此类推,排在第
,依此类推,排在第![]() 位的数称为第
位的数称为第![]() 项,记为
项,记为![]() .一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母
.一般地,若果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫作等比数列,这个常数叫作等比数列的公比,公比通常用字母![]() 表示
表示![]() ,如数列
,如数列![]() 为等比数列,其中
为等比数列,其中![]() ,公比
,公比![]() .
.
(材料二)为了求![]() 的值.可令
的值.可令![]()
则![]() , 因此
, 因此![]() ,所以
,所以![]() ,
,
即![]()
(1)等比数列![]() 的公比
的公比![]() 为_________,第6项是________
为_________,第6项是________
(2)如果一个数列![]() 是等比数列,且公比为
是等比数列,且公比为![]() ,那么根据定义可得到
,那么根据定义可得到![]() ,
,![]() ,
,![]() ,由此可得
,由此可得![]() (用
(用![]() 和
和![]() 的代数式表示)
的代数式表示)
(3)若某等比数列的公比![]() ,第2项
,第2项![]() ,则它的第1项
,则它的第1项![]() ,第4项
,第4项![]() ,并求出
,并求出![]() 的值.
的值.
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 内任取一点
内任取一点![]() ,连接
,连接![]() ,在⊿
,在⊿![]() 外分别以
外分别以![]() 为边作正方形
为边作正方形![]() 和
和![]() .
.
⑴.按题意,在图中补全符合条件的图形;
⑵.连接![]() ,求证:⊿
,求证:⊿![]() ≌⊿
≌⊿![]() ;
;
⑶.在补全的图形中,求证:![]() ∥
∥![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
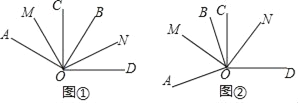
【题目】如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 . 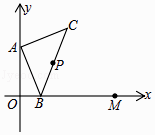
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,F是AD的中点,作
,F是AD的中点,作![]() ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论![]() ;
;![]() ;
;![]() ,
,![]() 中一定成立的是______
中一定成立的是______ ![]() 把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
(1)一个箱子,如果装橙子可以装18个,如果装梨可以装16个,现共有橙子、梨400个,而且装梨的箱子是装橙子箱子的2倍.请算一下,装橙子和装梨的箱子各多少个?
(2)一群小孩分一堆苹果,每人3个多7个,每人4个少3个,求有几个小孩?几个苹果?
(3)一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com