
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
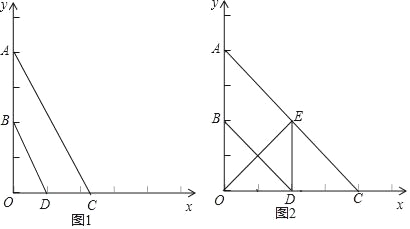
【答案】(1)BD∥AC;(2)点C的坐标为(![]() ,0);(3)直线AC的解析式为y=﹣x+4.
,0);(3)直线AC的解析式为y=﹣x+4.
【解析】试题分析:(1)由A与B的坐标求出OA与OB的长,进而得到B为OA的中点,而D为OC的中点,利用中位线定理即可得证;
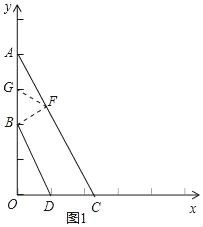
(2)如图1,作BF⊥AC于点F,取AB的中点G,确定出G坐标,由平行线间的距离相等求出BF的长,在直角三角形ABF中,利用斜边上的中线等于斜边的一半求出FG的长,进而确定出三角形BFG为等边三角形,即∠BAC=30°,设OC=x,则有AC=2x,利用勾股定理表示出OA,根据OA的长求出x的值,即可确定出C坐标;
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,进而得到DE垂直于OC,再由D为OC中点,得到OE=CE,再由OE垂直于AC,得到三角形AOC为等腰直角三角形,求出OC的长,确定出C坐标,设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出AC解析式.
试题解析:
(1)∵A(0,4),B(0,2),
∴OA=4,OB=2,点B为线段OA的中点,
又点D为OC的中点,即BD为△AOC的中位线,
∴BD∥AC;
(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),
∵BD∥AC,BD与AC的距离等于1,
∴BF=1,
∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,
∴FG=BG=![]() AB=1,
AB=1,
∴△BFG是等边三角形,∠ABF=60°.
∴∠BAC=30°,
设OC=x,则AC=2x,
根据勾股定理得:OA=![]() ,
,
∵OA=4,
∴x=![]() ,
,
∵点C在x轴的正半轴上,
∴点C的坐标为(![]() ,0);
,0);
(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,
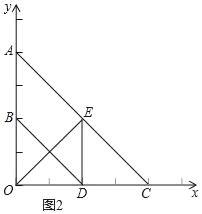
∴DE⊥OC,
∵点D为OC的中点,
∴OE=EC,
∵OE⊥AC,
∴∠OCA=45°,
∴OC=OA=4,
∵点C在x轴的正半轴上,
∴点C的坐标为(4,0),
设直线AC的解析式为y=kx+b(k≠0).
将A(0,4),C(4,0)代入AC的解析式得:
![]()
解得:![]()
∴直线AC的解析式为y=﹣x+4.


科目:初中数学 来源: 题型:
【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
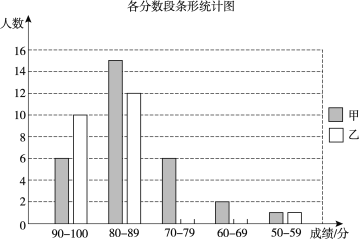
(1)请根据乙校的数据补全条形统计图;
(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,
请为他们各写出一条可以使用的理由;
甲校: .乙校: .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为cm2 . 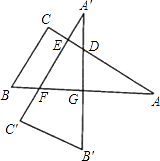
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 内任取一点
内任取一点![]() ,连接
,连接![]() ,在⊿
,在⊿![]() 外分别以
外分别以![]() 为边作正方形
为边作正方形![]() 和
和![]() .
.
⑴.按题意,在图中补全符合条件的图形;
⑵.连接![]() ,求证:⊿
,求证:⊿![]() ≌⊿
≌⊿![]() ;
;
⑶.在补全的图形中,求证:![]() ∥
∥![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
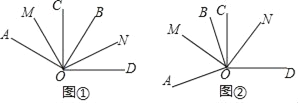
【题目】如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com