
【题目】已知△ABC中,AB=AC,现将△ABC折叠,使点A、B两点重合,折痕所在的直线与直线AC的夹角为40°,则∠B的度数为______°.
【答案】65°或25°
【解析】首先根据题意画出图形,如图1,如图1:由翻折的性质可知:EF⊥AB,所以∠A+∠AFE=90°,从而可求得∠A=50°,然后根据等腰三角形的性质和三角形的内角和定理可求得∠B=65°;如图2;由翻折的性质可知:EF⊥AB,∠D+∠DAE=90°,故此∠DAE=50°,然后由等腰三角形的性质和三角形的外角的性质可求得∠B=25°.
如图1:
由翻折的性质可知:EF⊥AB,
∴∠A+∠AFE=90°.
∴∠A=90°-40°=50°,
∵AB=AC,
∴∠B=∠C.
∴∠B=![]() ×(180°-∠A)=
×(180°-∠A)=![]() ×(180°50°)=65°;
×(180°50°)=65°;
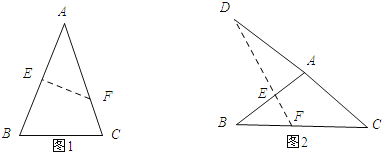
如图2;由翻折的性质可知:EF⊥AB,
∴∠D+∠DAE=90°.
∴∠DAE=90°-40°=50°,
∵AB=AC,
∴∠B=∠C.
∵∠B+∠C=∠DAE,
∴∠B=![]() ∠DAE=
∠DAE=![]() ×50°=25°.
×50°=25°.
故答案为:65°或25°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于F.
(1)直接写出线段OE与OF的数量关系;
(2)如图2,若点E在AC的延长线上,过点A作AM⊥BE ,AM交DB的延长线于点F,其他条件不变.问(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,说明理由;
(3)如图3,当BC=CE时,求∠EAF的度数.
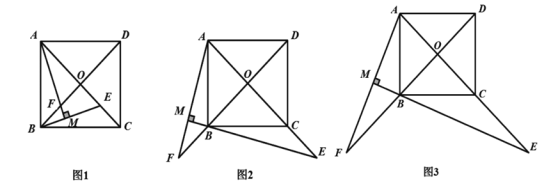
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③![]() +
+![]() =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;
④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年(1)班和八年(2)班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年(1)班 | 24 | 24 | |
八年(2)班 | 24 |
(2)你认为那个班的学生纠错的得分情况比较整齐一些,通过计算说明理由.
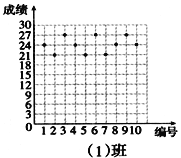
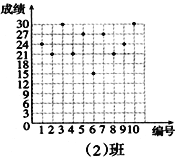
查看答案和解析>>
科目:初中数学 来源: 题型:
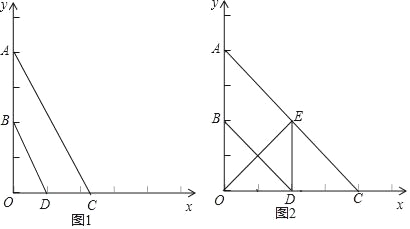
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com