
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).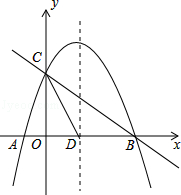
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
【答案】
(1)
解:把A(﹣1,0),C(0,2)代入y=﹣ ![]() x2+mx+n得
x2+mx+n得  ,解得
,解得  ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:存在.
抛物线的对称轴为直线x=﹣ 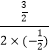 =
= ![]() ,
,
则D( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() =
= ![]() ,
,
如图1,当CP=CD时,则P1( ![]() ,4);
,4);
当DP=DC时,则P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,满足条件的P点坐标为( ![]() ,4)或(
,4)或( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )
) 
(3)
解:当y=0时,=﹣ ![]() x2+
x2+ ![]() x+2=0,解得x1=﹣1,x2=4,则B(4,0),
x+2=0,解得x1=﹣1,x2=4,则B(4,0),
设直线BC的解析式为y=kx+b,
把B(4,0),C(0,2)代入得 ![]() ,解得
,解得 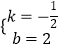 ,
,
C的解析式为y=﹣ ![]() x+2,
x+2,
设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),
x+2),
∴FE=﹣ ![]() x2+
x2+ ![]() x+2﹣(﹣
x+2﹣(﹣ ![]() x+2)=﹣
x+2)=﹣ ![]() x2+2x,
x2+2x,
∵S△BCF=S△BEF+S△CEF= ![]() 4EF=2(﹣
4EF=2(﹣ ![]() x2+2x)=﹣x2+4x,
x2+2x)=﹣x2+4x,
而S△BCD= ![]() ×2×(4﹣
×2×(4﹣ ![]() )=
)= ![]() ,
,
∴S四边形CDBF=S△BCF+S△BCD
=﹣x2+4x+ ![]() (0≤x≤4),
(0≤x≤4),
=﹣(x﹣2)2+ ![]() .
.
当x=2时,S四边形CDBF有最大值,最大值为 ![]() . ,此时E点坐标为(2,1)
. ,此时E点坐标为(2,1)

【解析】(1)直接把A点和C点坐标代入y=﹣ ![]() x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣
x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣ ![]() ,则D(
,则D( ![]() ,0),则利用勾股定理计算出CD=
,0),则利用勾股定理计算出CD= ![]() ,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1(
,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1( ![]() ,4);当DP=DC时,易得P2(
,4);当DP=DC时,易得P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() );(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣
);(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣ ![]() x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣
x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),则FE=﹣
x+2),则FE=﹣ ![]() x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF=
x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF= ![]() 4EF=﹣x2+4x,加上S△BCD=
4EF=﹣x2+4x,加上S△BCD= ![]() ,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+
,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+ ![]() (0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.
(0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.


科目:初中数学 来源: 题型:
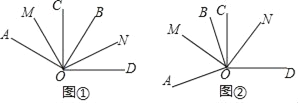
【题目】如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,F是AD的中点,作
,F是AD的中点,作![]() ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论![]() ;
;![]() ;
;![]() ,
,![]() 中一定成立的是______
中一定成立的是______ ![]() 把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
(1)一个箱子,如果装橙子可以装18个,如果装梨可以装16个,现共有橙子、梨400个,而且装梨的箱子是装橙子箱子的2倍.请算一下,装橙子和装梨的箱子各多少个?
(2)一群小孩分一堆苹果,每人3个多7个,每人4个少3个,求有几个小孩?几个苹果?
(3)一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )

A. 10 ° B .20 ° C .30° D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com