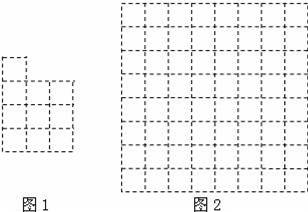
现有10个边长为1的正方形，排列形式如图1，请把它们分割后拼接成一个新的正方形．要求：在图1中用实线画出分割线，并在图2的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．
字词句段篇系列答案科目：初中数学 来源： 题型：
注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．
要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场．根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀多少个队参赛？
解题方案：
设比赛组织者应邀请x个队参赛，
（1）用含x的代数式表示：
那么每个队要与其他 个队各赛一场，又由于甲队对乙队的比赛和乙队对甲对的比赛是同一场比赛，所以全部的比赛一共有 场；
（2）根据题意，列出相应方程；
（3）解这个方程，得；
（4）检验： ；
（5）答： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法中正确的有（ ）
①位似图形都相似；
②两个等腰三角形一定相似；
③两个相似多边形的面积比为4：9，则周长的比为16：81；
④若一个三角形的三边分别比另一个三角形的三边长2cm，那么这两个三角形一定相似．
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，利用勾股定理即可把原图分割成四个斜边为
B．
D．
，再求当a=
﹣1时代数式的值．
