
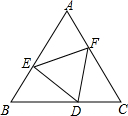
 如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$.
如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$. 分析 由于△ABC、△EFD都是等边三角形,因此它们的内心重合,设△ABC的内心为M,△AEF的内心为N,连接FN、MF,可先证MN=MF,而后由AN=MA-MN=MA-MF求出MA的值,易知∠NAF=30°,根据直角三角形的性质即可求出△AEF的内切圆半径.
解答 解:设△AEF的内切圆半径为r,
∵△ABC、△DEF都是等边三角形,且△DEF的三个顶点都在△ABC的边上,
∴△AEF≌△BDE≌△CFD,
∴AF=BE,AE+AF+EF=AE+BE+EF=3+2=5.
S△ABC=$\frac{1}{2}×3×\frac{\sqrt{3}}{2}×3$=$\frac{9\sqrt{3}}{4}$,S△DEF=$\frac{1}{2}×2×\frac{\sqrt{3}}{2}×2$=$\sqrt{3}$
∴S△AEF=$\frac{1}{3}$(S△ABC-S△DEF)=$\frac{1}{3}×(\frac{9\sqrt{3}}{4}-\sqrt{3})$=$\frac{5\sqrt{3}}{12}$.
∴r═$\frac{2{S}_{△AEF}}{AE+AF+EF}=\frac{2×\frac{5\sqrt{3}}{12}}{5}=\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题主要考查的是等边三角形的性质、三角形的内切圆、三角形的外角性质以及直角三角形的性质等知识,熟练掌握三角形的内切圆的半径与三角形的周长、面积之间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
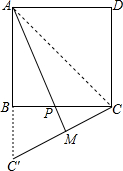 在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′.
在边长为1的正方形ABCD中,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C′. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 造型 | 甲 | 乙 |
| A | 90盆 | 30盆 |
| B | 40盆 | 100盆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com