
分析 根据题意,本题分三种情况,第一种是0°<α<90°,第二种是α=90°,第三种是90°<α<180°,然后画出相应的图形,即可解答本题.
解答 解:当0°<α<90°时,如下图所示: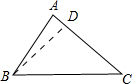
作BD⊥AC于点D,
∵在△ABC中,AB=a,AC=b,∠A=α,
∴BD=AB×sinα.
${S}_{△ABC}=\frac{AC×BD}{2}=\frac{b×asinα}{2}$=$\frac{absinα}{2}$.
当α=90°时,如下图所示: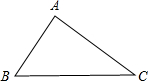
∵在△ABC中,AB=a,AC=b,∠A=α,
∴${S}_{△ABC}=\frac{AB×AC}{2}=\frac{ab}{2}$.
当90°<α<180°时,如下图所示: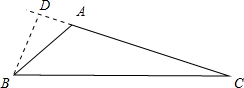
作BD⊥CA交CA的延长线于点D,
∵在△ABC中,AB=a,AC=b,∠A=α,
∴BD=AB×sin(180°-α)=asin(180°-α).
∴${S}_{△ABC}=\frac{AC×BD}{2}=\frac{basin(180°-α)}{2}$=$\frac{absin(180°-α)}{2}$.
点评 本题考查三角形的面积、锐角三角函数,数学中分类讨论思想的运用,关键是根据题意分析出三种情况.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
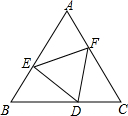 如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$.
如图,边长为2的正三角形DEF的三个顶点恰好在边长为3的正三角形ABC的各边上,则三角形AEF的内切圆的半径为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com